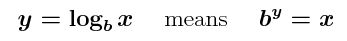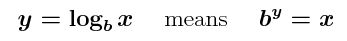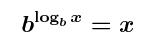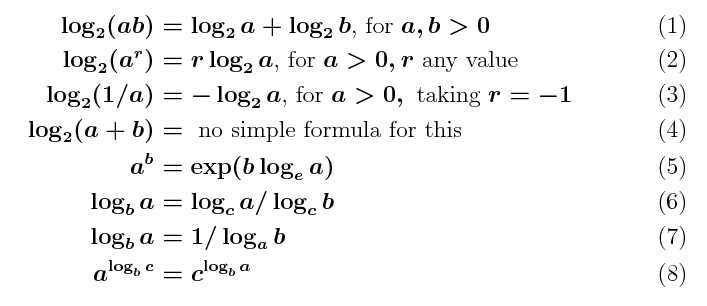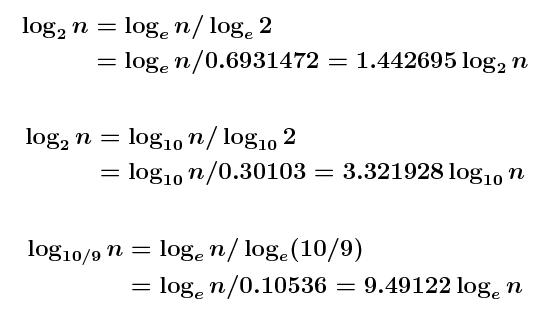CS 3343/3341
Analysis of Algorithms |
Logarithms |
[See your text, page 56.]
Definition of Logarithms.
By definition, the logarithm function is the inverse of
the exponential function, so that
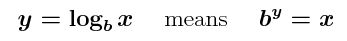 One says: ``y is the logarithm of
x to base b,'' or
``y is the log base
b of x.''
Stated another way, logbx (also known as
y) is the exponent you raise b to
in order to get x.
Thus
One says: ``y is the logarithm of
x to base b,'' or
``y is the log base
b of x.''
Stated another way, logbx (also known as
y) is the exponent you raise b to
in order to get x.
Thus
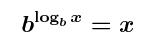
Logarithms base 2.
Logs base 2 are the favorite of computer scientists,
because binary numbers are used so often and because many
algorithms involve dividing things in two.
Of course, the official notation for log base 2 is:
log2 x. Your book uses lg x,
but this is not standard notation.
The only standard notation of this sort is to write
ln x for loge x
(In fact, Wikipedia says:
log2 n
is frequently written ld n, or lg n,
although the
ISO specification is that it should be lb (n),
lg (n) being reserved for
log10 n.
ld, lg, and lb are all a muddle
of non-standard notations, in spite of the ISO specs.)
So y = log2 x means the same as
2y = x. Another way to say this
is that a logarithm base 2 of x
is an exponent, namely it is the exponent you raise
2 to in order to get x.
In symbols: if y = log2 x, then
x = 2y =
2log2 x.
In particular 210 = 1024
means the same as log2 1024 = 10.
Notice that 2y > 0 for all
y and inversely log2 x
is not defined for x <= 0.
If you start with a positive integer n and repeatedly
divide it by 2 (truncated integer division), then after
roughly log2 n divisions, you get to 1
and then to 0. This fact often comes up in computer algorithms
since we often divide the size of the problem by 2.
Here are two tables of logs, base 2 and base 10:
| Logarithms base 2 |
|---|
| x = 2y =
2log2x |
y = log2x |
|---|
| 1 073 741 824 =
230 | 30 |
| 1 048 576 =
220 | 20 |
| 1 024 =
220 | 10 |
| 8 | 3 |
| 4 | 2 |
| 2 | 1 |
| 1 | 0 |
| 1/2 | -1 |
| 1/4 | -2 |
| 1/8 | -3 |
| 2-10 = 1/1024 | -10 |
| 0 | -infinity |
| < 0 | undefined |
| |
| Logarithms base 10 |
|---|
| x = 10y =
10log10x |
y = log10x |
|---|
| 1030 | 30 |
| 1020 | 20 |
| 1010 | 10 |
| 1000 | 3 |
| 100 | 2 |
| 10 | 1 |
| 1 | 0 |
| 1/10 | -1 |
| 1/100 | -2 |
| 1/1000 | -3 |
| 10-10 = 1/1010 | -10 |
| 0 | -infinity |
| < 0 | undefined |
|
Here are a few other formulas involving logarithms:
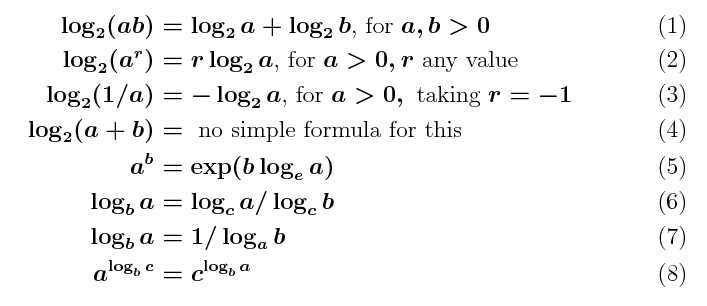 Equation (5) above is used to calculate
ab when only
functions base e are available.
(I used "exp(x)" above instead of "ex" to keep
the notation simpler.)
Similarly, equation (6) above allows one to find the
value of logb(a).
Here are further examples of the use of (6),
including your text's nasty expression
on page 176 and in Figure 7.4:
log10/9(n):
Equation (5) above is used to calculate
ab when only
functions base e are available.
(I used "exp(x)" above instead of "ex" to keep
the notation simpler.)
Similarly, equation (6) above allows one to find the
value of logb(a).
Here are further examples of the use of (6),
including your text's nasty expression
on page 176 and in Figure 7.4:
log10/9(n):
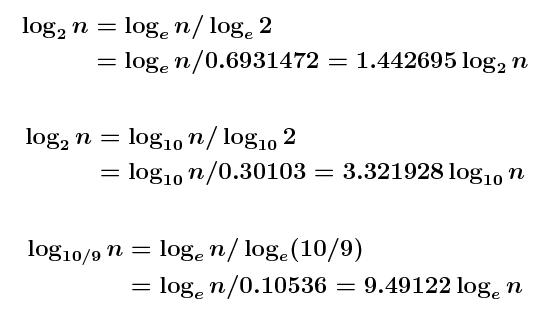
(Oops! At the right end of the second line above, it should
be loge instead of log2.)
Logs to one base are just a
constant times logs to another.
(In "big-Oh" notation the logs don't need a base specified.)
Some calculators, as well as languages like Java, do not directly
support logs base 2.
Java does not even support logs base 10,
but only logs base e, the ``natural'' log.
However, a log base 2 is just a fixed
constant times a natural log, so they are easy to calculate if
you know the ``magic'' constant. The formulas are:
log2 x =
(1 / loge2) loge x,
(mathematics)
= Math.log(x)/Math.log(2.0);
(Java). |
Here is the magic constant: loge(2) =
0.69314 71805 59945 30941 72321, or
1 / loge(2) = 1.44269 50408 88963 40735 99246.
(Similarly,
log2 x = log10(x) / log10(2),
and log10(2) =
0.30102 99956 63981.)
log2(x)
is the number of bits needed to represent x in binary.
Thus log210000 = 13.28771238, so it takes
14 bits to represent 10000 in binary.
(In fact, 1000010 = 100111000100002.)
Exact powers of 2 are a special case:
log21024 = 10, but it takes
11 bits to represent 1024 in binary,
as 10000000000.
Similarly, log10(x) gives how many decimal
digits are needed to represent x.
Last modified: 2012-07-12.
(Please use ISO
8601, the International Standard.)