CS 3343
 Analysis of Algorithms 
  Hamiltonian-Circuit   
  reduces to   
  Traveling-Salesman   
HC ≤p TS

Introduction. Before reading this page, you should first read The Class NP of Problems and NP-complete Problems. This present page first shows that Hamiltonian-Circuit (HC) reduces to Traveling-Salesman (TS), that is HC ≤p TS.

As a second example, this page then briefly indicates part of the proof that Vertex-Cover (VC) reduces to Hamiltonian-Circuit (HC), that is, VC ≤p HC.

First Example: HC ≤p TS. First define the Traveling-Salesman Problem.

Traveling-Salesman Problem (TS):

Start a complete undirected graph G=(V,E), and for each pair of vertices i and j a cost function c(i,j)>=0. A TS-tour is a circuit that visits each vertex exactly once. The total cost of the TS-tour is the sum of c(i,j) for each individual step from vertex i to vertex j.

The decision question is: Given an integer k, is there a TS-tour with total cost less than k?

The Hamiltonian Cycle Problem (HC) is defined at the start of the write-up Zero Knowledge Proofs.

In your text's presentation, they have already proved that HC is NP-complete, and they wish to show that TS is NP-complete. In order to do this, they need a polynomial reduction from HC to TS, that it, they must show that: HC ≤p TS. (They also need to show that TS is in NP, but we will often skip over this.)

To do this, we need a function from HC to TS. Start with an instance of HC, that is, start with an undirected graph G=(V,E). We must construct an instance of of TS: with an undirected graph G'=(V',E'), with cost function c(i,j), and with bound k. First let V' = V, so the vertices stay the same. Let E' be the set of all possible edges between any two distinct vertices in V. Thus G'=(V,E') is a complete graph with V the same as before, and with E' all possible edges. Let the cost function be defined by:

Let the bound k be |V|, the number of vertices.

To finish the proof, we must show that G has a Hamiltonian Cycle if and only if (exactly when) G' has a TS-tour of length at most k = |V|. But this is clear: if G has a HC, then this cycle will go along k edges in E, and as edges in E', these each have cost 1. So the total cost will k, giving a TS-tour with cost k.

On the other hand, suppose G' has a TS-tour with cost k (or less). Since k edges must have total cost adding up to k, each edge's cost must be 1, so these must be edges that are in E. Thus the TS-tour has to be a Hamiltonian Cycle.

Second Example: VC ≤p HC. Now define the Vertex-Cover Problem.

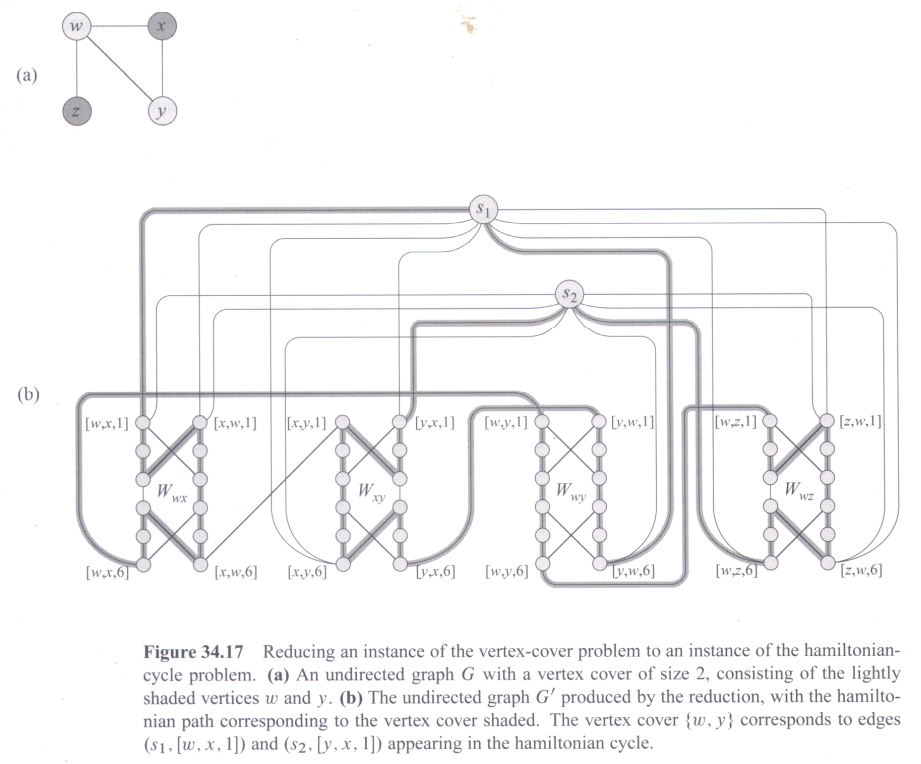
Vertex-Cover Problem (VC):

Start with an undirected graph G=(V,E), and a positive integer k. A vertex cover is a subset V' of V such that if (u,v) is an edge, then either u is in V' or v is in V' (or both). (Thus the vertices in V' "cover" at least one end of each edge.) The size of a vertex cover is the number of vertices in V', that is |V'|.

The decision question is: Given the integer k, is there a vertex cover of size equal to k?

Here I'm only giving your text's picture of a very simple example of the construction involved in proving that VC ≤p HC. It should be interesting for you to see how intricate these proofs can be, but the actual proof is over 4 pages long in your text, so I'm not going to try to present it.

For a proof, we must define a polynomial function from VC to HC. This means, for each specific problem instance in VC, we must define a problem instance in HC. The function must have the property that the answer to the VC instance is "Yes" if and only if (exactly when) the answer to the HC instance is "Yes". Your text has done up an illustration (part (a) below) starting with a graph with vertices {w,x,y,z} and undirected edges {(w,x),(w,y),(w,z),(x,y)}. This is a particularly simple example of VC. The set V'={w,y} works as a cover of size 2, and clearly there is no cover of smaller size.

Then in part (b) below, is the constructed instance of HC. Notice that we are not looking at all of HC here, but only a vanishingly small number of very special instances that correspond to every instance of VC.

The weird looking subgraphs above with 12 vertices in them are called widgets. They enforce certain properties on any Hamiltonian circuit. There is one widget for each edge of the VC instance. There are two other selector vertices in this HC instance: s1 and s2, corresponding to the two vertices in the cover V'. The widgets are linked together into two chains, one for the edges covered by w: (w,x), (w,y), and (w,z), and the other for the edges covered by y: (w,y) and (x,y). (The widgets are also linked into a chain for the edges covered by x and a chain (just one widget) for the edges covered by z.) Thus links give a path through each of the widgets in each chain. The chains overlap one another. Finally, each selector vertex is joined to the start and end of each chain. (Wheh!)

The widgets are constructed so that there are only three ways for a Hamiltonian path to go through them. The three ways are illustrated in the diagram. The proof continues by showing that the path through a given chain corresponds to the edges covered by one vertex, and the total circuit, if it is Hamiltonian, must correspond to a vertex cover of the original VC instance, since it includes every widget.

To state this another way, each selector includes a path through one chain (any one chain). Together a path through both selectors include paths through two chains. If it is a Hamiltonian path it must go through all widgets, and this means that the two chains include vertices that cover all edges.

Revision date: 2012-04-22. (Please use ISO 8601, the International Standard Date and Time Notation.)