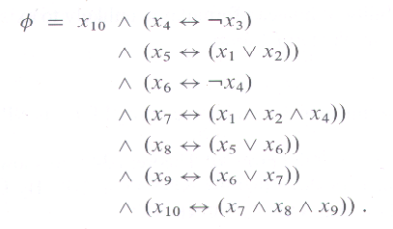
Click picture or here for full size image.
CS 3343 Analysis of Algorithms |
NP-Complete Problems (NPC)
|
Definition. A problem L is
NP-complete if
|
|
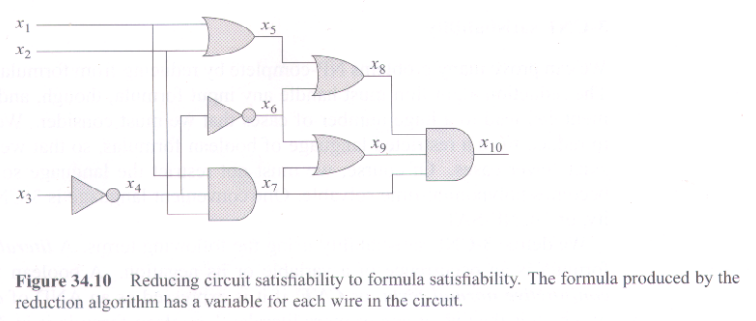
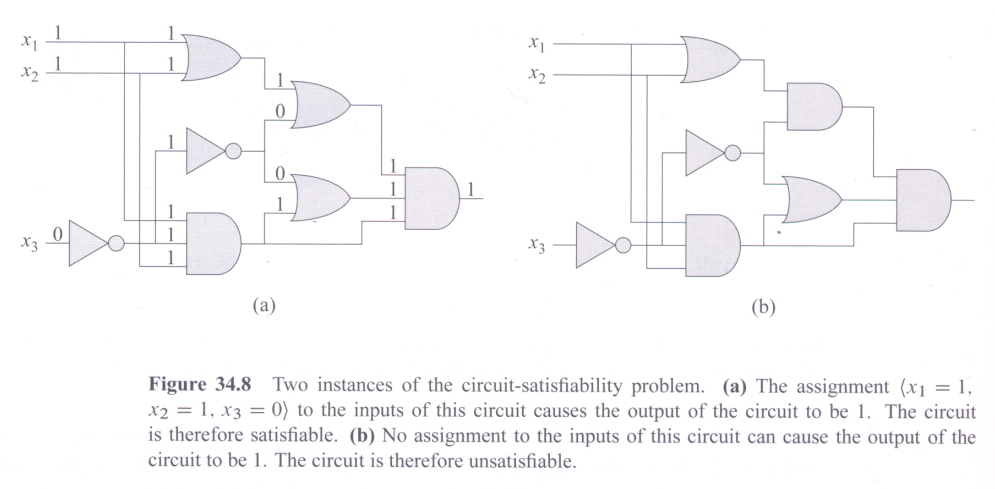
Circuit Satisfiability (CSAT):
Start with a circuit with AND, OR, and NOT gates, and with n inputs x1, x2, x3, ..., xn and one output. The decision question is: can we choose 0 or 1 values to assign to the inputs so that the output will be 1? |

(Formula) Satisfiability (SAT):
Start with a boolean formula with:
to the variables values so that the formula will evaluate to 1 (true)? |
To prove SAT is NP-complete,
prove that
|
|
To prove that a new problem L is NP-complete, we need only choose some suitable problem L' that is already known to be NP-complete and prove that
|