Newton's method is amazing because each iteration (each loop) doubles the number of correct digits of the answer.

Newton's Method is used to find successive approximations to the roots of a function. If the function is y = f(x) and x₀ is close to a root, then we usually expect the formula below to give x₁ as a better approximation. Then you plug the x₁ back in as x₀ and iterate.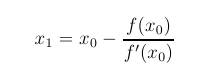

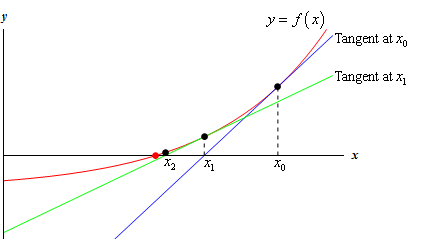
Here's an illustration of the method:

(click image for another illustration)

Following the link above (or here) illustrates another problem: Newton's method doesn't necessarily work well, or even work at all, unless you get to an initial guess that is close to the root.

A number of web pages explain how the above formula for Newton's method is derived. For example:

1. Newton's method (Wikipedia). Long complex article.
2. Newton's method. Simple pictorial explanation using Flash.
3. Newton's method (MIT course). Explanation in PDF.
4. Newton's method. Explanation and source for the illustration above.