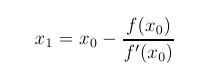
CS3343/3341
 Analysis of Algorithms 
Spring 2012
Weird Topic
  Newton's Method to   
  Perform Division  

Newton's Method:

Newton's Method is used to find successive approximations to the roots of a function. If the function is y = f(x) and x0 is close to a root, then we usually expect the formula below to give x1 as a better approximation. Then you plug the x1 back in as x0 and iterate. See Newton's Method for a derivation of the formula below.

Perform Division by d:

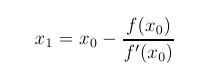
Suppose one wants to do division, say by a number d. It suffices to calculate the reciprocal of d, that is, 1/d. In order to calculate 1/d, use the function f(x) = 1/x - d, with 1/d as its root. Using Newton's method, one gets the equations:

Or just

As with the formula for square roots, this is an amazingly simple formula, given that it produces such good results. Notice also that the formula has only two multiplications and one subtraction.

The program below incorporates normalization and calculates the reciprocal of an arbitrary positive double. The important issue here is that this method does not use division, except for division by a power of two, which can be carried out very efficiently on a binary machine. An actual commercial software division routine would have many improvements and optimizations. The routine below only demonstrates the feasibility.

For convenience the input double is given as a command line argument. In the several example outputs, there is one very small positive number and one very large one.

In the data below, black digits are correct, while red digits are incorrect.

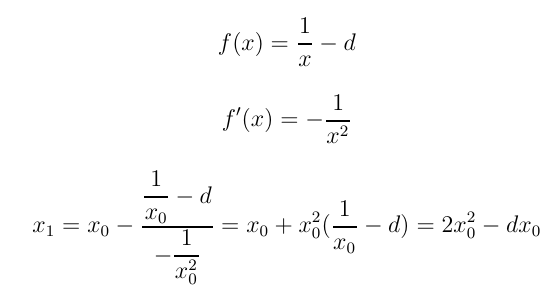
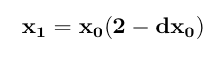
Newton's Method, division by the double d Outputs (red = incorrect digits)
// DivD: use Newton's method for 1/d
//  only divisions used are by 2
public class DivD {

   private double mul; // denormalizing factor

   // normalize to 0.5 <= d <= 1
   public double norm(double d) {
      // divide d by power of 2
      mul = 1.0; // power of 2
      double d0 = d;
      while (d0 > 1) {
         // divide by 2, will
         // later divide by 2 again
         d0 = d0/2.0;
         mul = mul*2.0;
      }
      while (d0 < 0.5) {
         d0 = d0*2.0;
         mul = mul/2.0;
      }
      // d0 now normalized
      return d0;
   }

   // denorm: reverse the normalization
   public double denorm(double invD0) {
      return invD0/mul;
   }

   // calculate 1/d0, 0.5 <= d0 <= 1
   public double invD(double d0) {
      // initial approx: 48/17 - 32/17*d0
      double x0 = 2.82353 - 1.88235*d0;
      System.out.println("1st approx to 1/d0:"+ x0);
      double x1;
      for ( ;  ;  ) {
         x1 = x0*(2 - d0*x0);
         System.out.println(x1);
         if (Math.abs(x1 - x0) < 1.0e-7) break;
         x0 = x1;
      }
      return x1;   
   }

   public static void main(String[] args) {
      // calculate 1/d for any d > 0
      DivD divD = new DivD();
      double d = Double.parseDouble(args[0]);
      System.out.println("d:" + d + ", want 1/d");
      // normalize to 0.5 <= d <= 1
      double d0 = divD.norm(d);
      // d0 now normalized
      System.out.println("normalized, d0:" + d0 +
         ", want 1/d0");
      double invD0 = divD.invD(d0);
      // denoramlize: divide invD0 by mul
      double invD = divD.denorm(invD0);
      System.out.println("1/" + d + " = \t" + invD);
      System.out.println("check on ans:\t" + 1.0/d);
   }
}

d:3.141592653589792, want 1/d  (d = π)
normalized, d0:0.785398163397448, want 1/d0
1st approx to 1/d0:1.3451357671288138
1.2691797691683022
1.273226599977265
1.2732395446035567
1.2732395447351632
1/3.141592653589792 = 0.3183098861837908
check on ans:         0.3183098861837908

d:13.0, want 1/d
normalized, d0:0.8125, want 1/d0
1st approx to 1/d0:1.294120625
1.2275083439590577
1.230760591145715
1.2307692307085834
1.2307692307692308
1/13.0 =        0.07692307692307693
check on ans:   0.07692307692307693

d:0.003247, want 1/d
normalized, d0:0.831232, want 1/d0
1st approx to 1/d0:1.2588604448
1.2004429185386936
1.2030279906583141
1.2030335694228516
1.2030335694487218
1/0.003247 =    307.97659377887277
check on ans:   307.9765937788728

d:2.718281828459045E-8, want 1/d  (d = e*10E-8)
normalized, d0:0.912104027698647, want 1/d0
1st approx to 1/d0:1.1066309834614518
1.096270065456504
1.0963661621352847
1.0963661705596517
1/2.718281828459045E-8 = 3.6787944117144234E7
check on ans:            3.6787944117144234E7

d:4.812118250596034E14, want 1/d (d=ln(φ)*10E15)
normalized, d0:0.8548039166449033, want 1/d0
1st approx to 1/d0:1.2144898475034662
1.1681562359459892
1.1698564572793013
1.1698589355094466
1.1698589355146964
1/4.812118250596034E14 = 2.0780869212350276E-15
check on ans:            2.078086921235028E-15

Revision date: 2011-12-03. (Please use ISO 8601, the International Standard Date and Time Notation.)