[See Hamiltonian Paths for introductory material.]
It is feasible to carry out a simple backtracking search of all Hamiltonian Paths (HPs) starting at ME. The results agree completely with Knuth. This page shows code and results for such a search.

Knuth's methods are far more powerful than this straightforward approach, will handle cases where brute force search is not feasible, and produce much more information.

First, for reference I give the map of state capitals with the number of each node, rather than the two-character id:

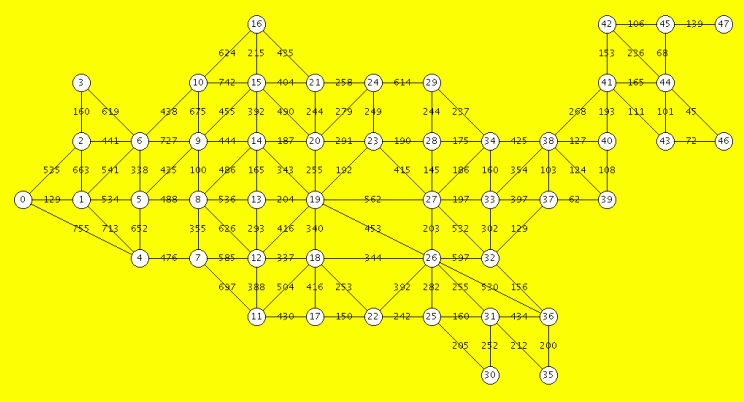A naive search for all HPs would hardly be feasible without first noting that vertex 47 is isolated, so each HP must start or end at 47. We choose to start all HPs at 47. Next, vertex 41 is an "articulation point" of the graph, so that all paths are broken into 2 independent portions: first from 47 to 41, and then on from 41. Moreover, there is only one path from 47 to 41 that includes all the vertices. The diagram at the left below shows a study of all 8 possible paths starting at 47 and ending at 41, with only 47-45-42-44-46-43-41 including all the vertices (outlined in green; the others are outlined in blue). The list of output data at the very end omits these first 7 vertices, since they all start this way.

With this simplification, the search took about 48 hours on my (slow) PC at home. Without simplifying this way, the search would have lasted 16 days.

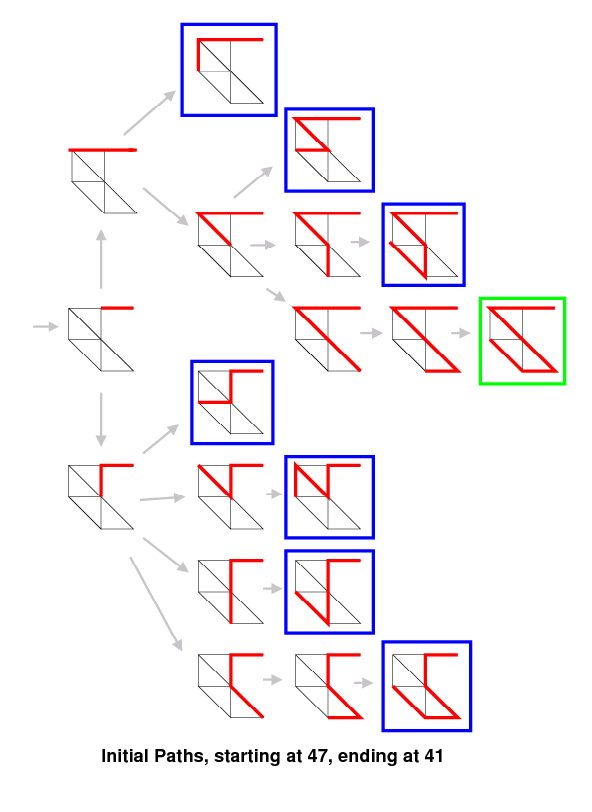
Graph from 47 to 41, Image: PDF

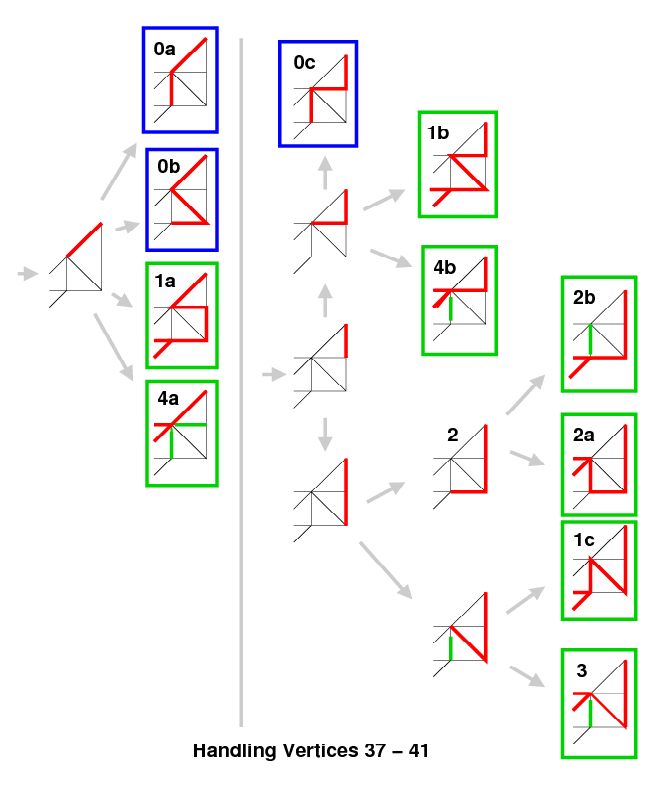
Graph including 37-41, Image: PDF

The diagram at the right above represents my work of shortening the search further by focusing on the next collections of vertices. I eliminated dead ends (outlined in blue) and found duplicate searches that only needed to be performed once. For example, the HPs starting with the part labeled "1a", "1b", or "1c" are identical collections of 12731069 HPs, differing only in the initial vertices and in the initial start lengths. A green edge in a diagram is one that needs to be deleted from the graph by hand. Thus with care (and hand computation), a search through about 25 million HPs could be eliminated. There are similar savings elsewhere: eliminating the three "deadend" searches (inside a blue box), saving the processing equivalent of another 39 million HPs. But this whole approach was so complicated and error-prone (and it only saved about half the execution time) that I'm not presenting it. However, at the right is data about the different search portions (numbers in parentheses are for duplicate portions with different starting segments):

Portion Ham. Paths 1a 12731069   1b (12731069) 1c (12731069) 2a 13432384   2b 7918239   3 8145805   4a 483194   4b (483194) Total 68656026

Finally, here is the program to do the actual straightforward search.

Backtracking Search, all Hamiltonian Paths

// GraphMain.java: Controls Graph Program import java.io.*; public class GraphMain { public static void main(String[] args) { Graph ham = new Graph( "capsdist.txt"); // graph.printGraph(); ham.hamPathsStart(); // start at Maine } } // Graph.java: set up graph data structure import java.io.*; import java.util.Scanner; public class Graph { private int count; // number of nodes private Scanner sc; // input file name private GraphNode[] graph; private int calls; // for debugging private int bigCalls; // calls/1000000 private int paths; // count the ham paths private int maxPathLen; private int minPathLen; private IntStack st; private void err(int code) { System.exit(code); } public Graph(String fileName) { calls = 0; bigCalls = 0; paths = 0; maxPathLen = 0; minPathLen = 99999999; int num1 = 0, num2 = 0, num = 0; try { sc = new Scanner(new File(fileName)); } catch (Exception exception ) { err(1); } // get count = num of vertices if (sc.hasNextInt()) count=sc.nextInt(); else err(2); st = new IntStack(count + 5); graph = new GraphNode[count]; for (int i = 0; i < count; i++) graph[i] = new GraphNode(); while (sc.hasNextInt()) { num1 = sc.nextInt(); if (sc.hasNextInt()) num2 = sc.nextInt(); else err(2); if (sc.hasNextInt()) num = sc.nextInt(); else err(3); // undirected, insert both ways insert(num1, num2, num); insert(num2, num1, num); } } private void insert(int num1, int num2, int dist) { // patch the new node in at the start if (graph[num1].firstEdgeNode == null) { EdgeNode enode = new EdgeNode(num2, null, dist); graph[num1].firstEdgeNode = enode; } else { EdgeNode enode = new EdgeNode(num2, graph[num1].firstEdgeNode, dist); graph[num1].firstEdgeNode = enode; } } public void printGraph() { for (int i = 0; i < count; i++) { System.out.print(i + ": "); EdgeNode node=graph[i].firstEdgeNode; while (node != null) { System.out.print("[" + node.vertexNum + "," + node.edgeDist + "]"); node = node.nextEdgeNode; if (node != null) System.out.print(","); else System.out.print("\n"); } } } public void hamPathsStart() { st.push(47); st.push(45); st.push(42); st.push(44); st.push(46); st.push(43); graph[42].color = 2; graph[43].color = 2; graph[44].color = 2; hamPaths(41, 709, 6); System.out.println("Paths: " + paths); } // hamPaths: recursive path search from s public void hamPaths(int u, int pathLen, int edges) { // init u = 47 // limit # of calls initially calls++; if (calls > 1000000) { calls = 0; bigCalls++; } // save on stack to recover st.push(u); if (edges == 47) { if (pathLen < 11800) { System.out.print("Low len, " + pathLen + ": "); st.printStack(7); } else if (pathLen > 17940) { System.out.print("High len, " + pathLen + ": "); st.printStack(7); } if (pathLen < minPathLen) { minPathLen = pathLen; System.out.println("New Min, " + pathLen + ", paths: " + paths); } if (pathLen > maxPathLen) { maxPathLen = pathLen; System.out.println("New Max, " + pathLen + ", paths: " + paths); } paths++; if (paths%1000000 == 0) { System.out.println(paths + ", maxPathLen:" + maxPathLen + ", minPathLen:" + minPathLen); } } // if called, then color = 0 graph[u].color = 2; // black // work on adj. list EdgeNode vnode = graph[u].firstEdgeNode; // try each white vertex in turn int v = vnode.vertexNum; while(true) { if (graph[v].color == 0) { // white int edgeDist = edgeDistance(u, v); // recursive call! hamPaths(v, pathLen + edgeDist, edges + 1); // returned from God knows where } // move on to next vert in adj list vnode = vnode.nextEdgeNode; if (vnode == null) break; else v = vnode.vertexNum; } // all done with adj list graph[u].color = 0; // white // also pop stack for recovery st.pop(); } // end of hamPaths function

public int edgeDistance(int v1, int v2) { if (v1 < 0 || v1 > graph.length-1) return -1; if (graph[v1] == null) return -1; EdgeNode node =graph[v1].firstEdgeNode; while (node != null) { if (node.vertexNum == v2) return node.edgeDist; node = node.nextEdgeNode; } return -1; } public int pathLength(int[] path) { int dist = 0; for (int i = 0; i < path.length-1;i++){ int temp = edgeDistance(path[i], path[i+1]); if (temp == -1) return -1; dist += temp; } return dist; } } // end of Graph.java // GraphNode.java: node for graph's vertex // Holds vertex info, link to adj. list public class GraphNode { public EdgeNode firstEdgeNode; // other vertex info here public int color; // 0 = white, 2 = black public GraphNode() { firstEdgeNode = null; // initialize other vertex info here color = 0; } // just to force a class file public static void main(String[] args) { GraphNode g = new GraphNode(); } } // EdgeNode.java: holds graph's edge info // Implement adjacency list public class EdgeNode { public int vertexNum; // vertex num public EdgeNode nextEdgeNode; // next public int edgeDist; // edge length // other edge info here public EdgeNode(int num, EdgeNode node, int dist) { vertexNum = num; nextEdgeNode = node; edgeDist = dist; // initialize other edge info here } } // Stack: simple stack of ints public class IntStack { private int[] stack; // stack itself private int top; // current # of elements private final int size; // maximum size // IntStack: constructor public IntStack (int s) { top = 0; size = s; stack = new int[size]; // allocation } // pop: remove top element and return it public int pop() { if (top > 0) { return stack[--top]; } else { System.out.println("Underflow"); return 0; } } // push: push parameter onto stack public void push(int x) { if (top < stack.length) stack[top++] = x; else System.out.println("Overflow"); } // empty: is stack empty? public boolean empty() { return top == 0; } // full: is stack full? public boolean full() { return top >= stack.length; } // printStack: short form public void printStack() { for (int i = 0; i < top; i++) { System.out.print(stack[i] + " "); if ( i%20 == 19 ) System.out.println(); } System.out.println(); } public static void main(String[] args) { IntStack stack = new IntStack(500); stack.push(3); System.out.println(stack.pop()); } } Some extra data stuck in here: % cat capsdist.txt 48 0 4 755 0 1 129 0 2 535 1 4 713 1 5 534 1 6 541 1 2 663 2 6 441 2 3 160 3 6 619 4 7 476 4 5 652 5 8 488 5 9 435 5 6 338 6 9 727 6 10 438 7 11 697 7 12 585 7 8 355 8 12 626 8 13 536 8 14 486 8 9 100 9 14 444 9 15 455 9 10 675 10 15 742 10 16 624 11 17 430 11 18 504 11 12 388 12 18 337 12 19 416 12 13 293 13 19 204 13 14 165 14 19 343 14 20 187 14 15 392 15 20 490 15 21 404 15 16 215 16 21 435 17 22 150 17 18 416 18 22 253 18 26 344 18 19 340 19 26 453 19 27 562 19 23 192 19 20 255 20 23 291 20 24 279 20 21 244 21 24 258 22 25 242 22 26 392 23 27 415 23 28 190 23 24 249 24 29 614 25 30 205 25 31 160 25 26 282 26 31 255 26 36 530 26 32 597 26 27 203 27 32 532 27 33 197 27 34 186 27 28 145 28 34 175 28 29 244 29 34 237 30 31 252 31 35 212 31 36 434 32 36 156 32 37 129 32 33 302 33 37 397 33 38 354 33 34 160 34 38 425 35 36 200 37 39 62 37 38 103 38 39 124 38 40 127 38 41 268 39 40 108 40 41 193 41 43 111 41 44 165 41 42 153 42 44 236 42 45 106 43 46 72 43 44 101 44 46 45 44 45 68 45 47 139

The above program carries out the search through all possible ham paths. During the search, after each HP is found, the program prints a new shorter path (if the one discovered is shorter than what came before), and similarly a new longer path. This strategy could miss the second shortest and longest paths, but I also printed all paths shorter than a certain length and all paths longer than a certain length. Below I also printed a "milestone" line each time the number of paths discovered was divisible by 1000000.

Here are the unique two shortest HPs and the unique two longest HPs:

Two Shortest and two Longest Hamiltonian Paths

Longest: 18040: 47 45 42 44 46 43 41 40 39 37 33 38 34 28 29 24 21 16 10 15 20 23 27 32 26 36 35 31 30 25 22 18 17 11 7 12 8 13 19 14 9 5 4 0 2 1 6 3 # paths: 2793440, maxPathLen:18040 2nd longest: 18031: 47 45 42 44 46 43 41 40 39 37 33 38 34 28 29 24 23 20 15 21 16 10 9 14 19 27 32 26 36 35 31 30 25 22 18 17 11 7 12 13 8 5 4 0 2 1 6 3 # paths: 2495043, maxPathLen:18031 Shortest: 11698: 47 45 42 44 46 43 41 40 38 39 37 32 36 35 31 30 25 22 17 11 12 18 26 27 33 34 29 28 23 19 13 14 20 24 21 15 16 10 6 5 9 8 7 4 1 0 2 3 # paths: 11692399, minPathLen:11698 2nd shortest: 11720: 47 45 42 44 46 43 41 40 39 38 37 32 36 35 31 30 25 22 17 11 12 18 26 27 33 34 29 28 23 19 13 14 20 24 21 15 16 10 6 5 9 8 7 4 1 0 2 3 # paths: 11692399, minPathLen:11720

Here is a Python program that reads a file containing a separate list of cities on each line and produces the length of the path, using a distance dictionary. Of course I can get path lengths inside the main program, but it was convenient to be able to find the length of a given path.

Length of a path

# pathLen.py: calc length of path through cities import sys debug = False d = {( 0, 4):755, ( 0, 1):129, ( 0, 2):535, ( 1, 4):713, ( 1, 5):534, ( 1, 6):541, ( 1, 2):663, ( 2, 6):441, ( 2, 3):160, ( 3, 6):619, ( 4, 7):476, ( 4, 5):652, ( 5, 8):488, ( 5, 9):435, ( 5, 6):338, ( 6, 9):727, ( 6, 10):438, ( 7, 11):697, ( 7, 12):585, ( 7, 8):355, ( 8, 12):626, ( 8, 13):536, ( 8, 14):486, ( 8, 9):100, ( 9, 14):444, ( 9, 15):455, ( 9, 10):675, (10, 15):742, (10, 16):624, (11, 17):430, (11, 18):504, (11, 12):388, (12, 18):337, (12, 19):416, (12, 13):293, (13, 19):204, (13, 14):165, (14, 19):343, (14, 20):187, (14, 15):392, (15, 20):490, (15, 21):404, (15, 16):215, (16, 21):435, (17, 22):150, (17, 18):416, (18, 22):253, (18, 26):344, (18, 19):340, (19, 26):453, (19, 27):562, (19, 23):192, (19, 20):255, (20, 23):291, (20, 24):279, (20, 21):244, (21, 24):258, (22, 25):242, (22, 26):392, (23, 27):415, (23, 28):190, (23, 24):249, (24, 29):614, (25, 30):205, (25, 31):160, (25, 26):282, (26, 31):255, (26, 36):530, (26, 32):597, (26, 27):203, (27, 32):532, (27, 33):197, (27, 34):186, (27, 28):145, (28, 34):175, (28, 29):244, (29, 34):237, (30, 31):252, (31, 35):212, (31, 36):434, (32, 36):156, (32, 37):129, (32, 33):302, (33, 37):397, (33, 38):354, (33, 34):160, (34, 38):425, (35, 36):200, (37, 39): 62, (37, 38):103, (38, 39):124, (38, 40):127, (38, 41):268, (39, 40):108, (40, 41):193, (41, 43):111, (41, 44):165, (41, 42):153, (42, 44):236, (42, 45):106, (43, 46): 72, (43, 44):101, (44, 46): 45, (44, 45): 68, (45, 47):139 } f = open("highlow.txt",'r') for line in f: sys.stdout.write(line) t = line.split() sum = 0 for i in range(0,len(t)-1): if debug: sys.stdout.write(t[i] + ", " + t[i+1]) c1 = int(t[i]) c2 = int(t[i+1]) if c1 < c2: out = d[(c1,c2)] else: out = d[(c2,c1)] if debug: sys.stdout.write(", " + str(out) + '\n') sum += out sys.stdout.write(str(sum) + '\n')

One input file is highlow.txt, and the corresponding output is in the file highlow.html.

Finally, here are the results of the search: