Use Newton's laws to determine the forces on each body due to all other bodies. Then over a small time increment, each body gets a change to its location and velocity determined by the sum of those forces. The increment is chosen quite small. If chosen small enough, this approach should provide answers arbitrarily close to reality, assuming "reality" means the motion of point masses under Newtonian physics.

It's interesting that there is such a simple approximation algorithm, but no actual general solution for more than 2 bodies, and only a few specialized solutions, with the next two sections describing one such solution. The program here is just a "toy" version, but more elaborate approaches allow very accurate calculations of complicated systems (even of our solar system). All algorithms (with a few exceptions) are good for only a limited time into the future.

The code for this simulation was written as Java apps. It was modeled after a similar program in a hobby magazine. These still run, but browsers mostly don't support Java apps anymore. My Linux system (with a complete Java system loaded in), would let the applet be explicitly called with "appletviewer".

This software models three dimensions. On reflection, I realized that displaying a 3-D interaction would be difficult for me. Also, the interaction I was initially interested in was strictly 2-D. So I made everything zero in the third dimension. That shouldn't have affected the next section, but it might have affected the later 3-star interactions.

When I wrote the program here, I tested it out with two stars, and they rotated nicely in ellipses about their common center of gravity. I tried the stable configurations of two stars with a planet close to one of them (worked fine), and with a planet at quite a distance from them both (also worked fine). I also tried 3 stars, 2 in a binary system and a third coming in from the outside. I had seen an article describing this motion: usually there is too much energy for the third to be captured, but instead, sometimes after an incredible amount of chaotic motion, one of the stars is ejected to infinity, with a binary system remaining. Any one of the three might be ejected. (See three examples below under "Triple Star Systems".)

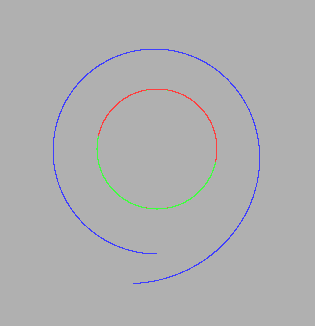
Finally, I tried out a system similar to and simpler than Asimov's story. I used two stars with equal mass, and a planet with zero mass. The stars rotated about each other in a perfectly circular orbit. (This is the red-green circle below.) I carefully started out the planet at the third vertex of an equilateral triangle, with the proper vector for its motion. (This is the blue orbit below. The initial position has the two stars at opposite ends of a horizontal diameter, with the blue planet directly below them at the third vertex of an equilateral triangle.) It would stay at the vertex of the triangle for much of one rotation, and then drift into chaos. I thought that something was wrong with my approach or with my equations. See Figure 1 below for snapshots of this situation:

Figure 1.

• 2 stars: green and red, of equal mass, each rotating in the same exact circle about their common center of gravity,
• 1 planet: blue, of negligible mass, starting at the Lagrange Point, with the proper velocity vector.
• The initial position of the two stars is on the circle at the center, where the red changes to green. The line through them is horizontal.
• The initial position of the planet is directly below the stars at the third vertex of an equilateral angle. It starts with the correct velocity and direction.
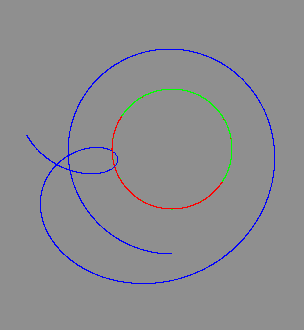
• The planet stays in the L5 position for most of one rotation (see first image above), but then it deviates more and more, even looping around one of the stars during the early part of its second rotation (see second image above).
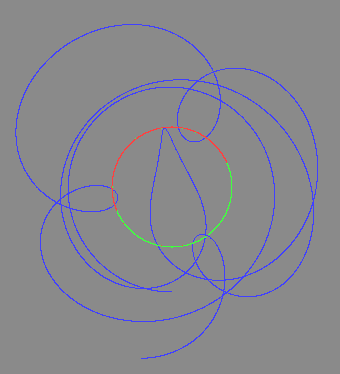
• After a chaotic orbit, the planet is eventually ejected to infinity (third picture above).

Note that I didn't check the "to infinity" part above. It went off a long way. My simulation is only approximate, of course. In the chaotic orbit above, the planet several times gets very close to one of the stars -- once extremely close. I may have needed to make my stepsize smaller to get the orbit closer to reality. I emphasize that I never did any careful checks about how close my simulation was to Newtonian physics.

        VIDEO OF LAGRANGE SYSTEM (going on from the second picture above)

(25 + sqrt(25*25 - 2^2))/2 = 24.95993579437711...,
    or approximately  24.96,
    or even very close to  25

The earth-moon and the sun-Jupiter system each exceed this ratio, and so they have stable Lagrange Points:

earth mass/moon mass  =  5.98 x 1024 kg / 7.35 x 1022 kg =   81.36
sun mass/jupiter mass = 1.989 x 1030 kg / 1.90 x 1027 kg = 1046

The number 24.96 is an interesting dimensionless constant, a product of basic (but very complex) Newtonian physics.

Going back to my simulation, I couldn't get a stable orbit with the ratio close to 25 , but I was able to get it easily at ratios above 50 . In our actual solar system, the earth-moon L4 and L5 points are fairly stable, but perturbations from the sun's large mass have the most effect. With the sun-jupiter system, there are two sets of asteroids in the asteroid belt (called the trojans) that move along in the L4 and L5 stable locations, ahead of and behind Jupiter and moving along with it.

Figure 2 shows a run with two stars having a mass ratio of 100 and a planet with negligible mass at the stable Lagrange Point:

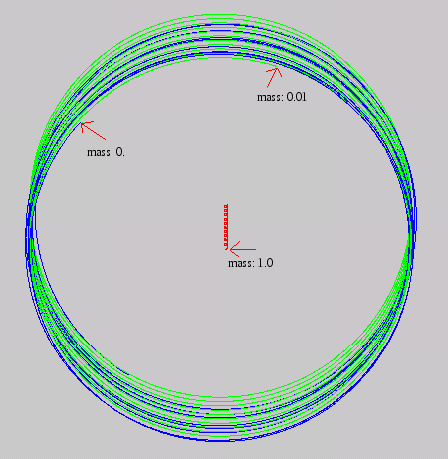
Figure 2.

• 2 stars: green with mass 0.01 and red with mass 1.0. Red (almost exactly at the center of mass) is nearly stationary, wobbling and drifting downward very slowly, while green goes in a circular orbit about red.
• 1 planet: blue, of mass 0.000005, starting at the Lagrange Point, with the proper velocity vector.
• The arrows show the positions of all three bodies after about 10 revolutions. They are still in the Lagrange configuration.

Figure 3 shows a run with a similar configuration, except that here there are 2 planets (each blue), one in each of the two stable Lagrange points. Again the 4 arrows show the positions of the two stars and the two planets after about 12 revolutions.

Figure 3.

Many double stars would not have as big a ratio, so their Lagrange points would not be stable. All these facts are explained in detail in the following articles:

References about Lagrange points (extremely thorough and sophisticated):

• Wikipedia article on Lagrange Points
• Stabbility Web Page About Lagrange Points
• Stability of Lagrange Points

It's interesting that as of 2023-09-10, the Wikipedia article about Asimov's Sucker Bait story does not say that the configuration in the story is impossible. Lagrange published his astonishing discovery in 1772. Ever since it's been known by most astronomers and physicists. Asimov was an actual scientist, with a 1948 PhD in Chemistry from Columbia University, so there's not much excuse for his mistake.

Suppose one tries to rescue the story. One could imagine a binary system with one red star having 0.1 solar masses, and another bright star with 3 solar masses. The mass ratio is 30 , so this works. You still have to wonder how the planet got into position, but in Asimov's story, this was the only such planet known, so it was presented as very rare. Another problem is that the planet had evolved life. Many people feel that even small red suns might have planets around them with life, and certainly the red sun would last long enough for this to happen (such a small red star lasts much longer than our sun). However the large star in the system would have a lifespan of well under half a billion years -- perhaps not enough time for life to develop. Oh well, one should ignore that and just make the important correction to the story.

The first two examples show three stars of equal mass, while in the third example, the "interloper" star has one-tenth the mass of the other two.

First System.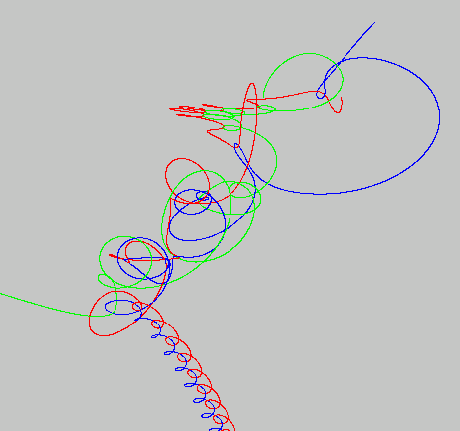

Figure 4.

• 3 stars: Green, Red, and Blue, of equal mass.
• Red and Green form a binary system, while Blue is an interloper, coming in from the upper right. (By the time this gets started, blue has already partly disrupted green and red.)
• After a chaotic interaction, Green is ejected off to the left, while Blue and Red form a new binary system that leaves at the bottom.

        VIDEO OF FIRST SYSTEM

Second System.

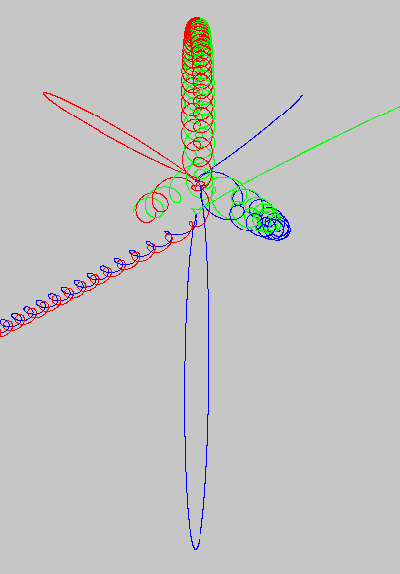
Figure 5.
Very similar to Figure 4.

• 3 stars: Green, Red, and Blue, of equal mass.
• Red and Green form a binary system, originally coming from the middle, moving right and upward. (As before, you just barely see green and red, coming in from the left and encountering blue.)
• Blue is an interloper, coming in from the upper right.
• First Red is thrown into a small orbit (toward the upper left), while Blue and Green rotate about one another (toward the lower right).
• Then Blue is thrown out into a larger orbit (straight down), while Red and Green rotate about one another (toward the top).
• Finally, Green is ejected to infinity off to the upper right, while Blue and Red form a new binary system that leaves toward the lower left.

Third System.

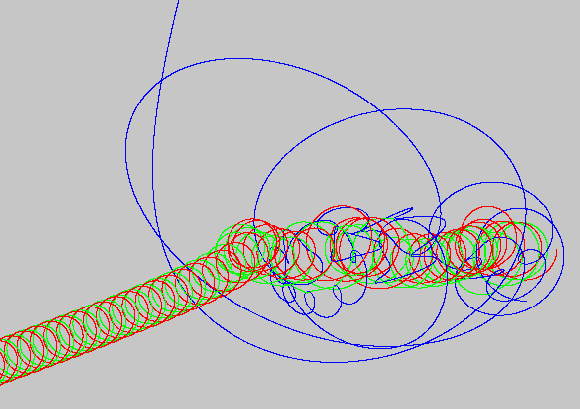
Figure 6.

• Red and Green have mass 1 , while Blue has mass 0.1 . (This one is interesting because here, instead of three equal masses, blue only has 10% the mass of the other two. Nevertheless blue manages to disrupt red and green, even with it's small mass.)
• Blue starts at the unstable Lagrange L5 point, with the correct initial velocity.
• Blue stays at the Lagrange L5 point for most of one revolution, and then drifts off. (You can clearly see the start of blue.)
• Blue goes through a chaotic orbit, and as mentioned above, affects the orbits of Red and Green significantly, even with its small mass.
• Finally, Blue is ejected to infinity (upward), and Red and Green continue toward the left without Blue.

Here is all the code, given as four listings: All the code

(Revision date: 2025-01-18. Please use ISO 8601, the International Standard.)