| |
 |
|
Python |
10.2 Graph Algorithm:
Knight's Tour |
|
Knight's Tour:
A knight's tour is sequence of knight moves on an
N-by-N chess board that visits each square
exactly once and ends where it started. This is called a
Hamiltonian Cycle of the board, using knight moves.
Such cycles exist only
for N even and greater than or equal to 6.
| 5 | |
30
(5,0) |
31
(5,1) |
32
(5,2) |
33
(5,3) |
34
(5,4) |
35
(5,5) |
|---|
| 4 | |
24
(4,0) |
25
(4,1) |
26
(4,2) |
27
(4,3) |
28
(4,4) |
29
(4,5) |
|---|
| 3 | |
18
(3,0) |
19
(3,1) |
20
(3,2) |
21
(3,3) |
22
(3,4) |
23
(3,5) |
|---|
| 2 | |
12
(2,0) |
13
(2,1) |
14
(2,2) |
15
(2,3) |
16
(2,4) |
17
(2,5) |
|---|
| 1 | |
6
(1,0) |
7
(1,1) |
8
(1,2) |
9
(1,3) |
10
(1,4) |
11
(1,5) |
|---|
| 0 | |
0
(0,0) |
1
(0,1) |
2
(0,2) |
3
(0,3) |
4
(0,4) |
5
(0,5) |
|---|
|
| | | 0 | 1 | 2 |
3 | 4 | 5 |
|---|
| |
The board has N rows and N columns, each numbered
from 0 to N-1. The squares are also numbered sequentially
from 0 to N*N-1, inclusive (the red
numbers). So a square is also given by a pair of
integers, giving row first and then column (the green
pairs). Thus (2,4) is row 2 and
column 4.
In case N is 6 (as shown at the left),
this is also square 16.
Here are functions to convert back
and forth between the two ways to represent a square:
def itot(i): # 0 <= i < N
return (i//N, i%N)
def ttoi(t): # 0 <= t[i] < 6, i = 0, 1
return t[0]*N + t[1]
At the left is a 6-by-6 board.
|
Below is a program that first constructs the graph for
the tour, and then carries out a recursive backtracking search
for paths starting at a given node. The search space is so large
that this is not a very satisfactory approach.
The program uses the list moves to find the next knight moves.
Here it adds or subtracts either 2 or 3 from the previous
coordinates, and then checks if the result is still on the
board -- up to 8 legal moves. (I'm still going to try other
possible kinds of knight moves someday. These are called
"grasshoppers".)
The program starts at square 0. There are only two moves next,
and then only two ways to finsh a circuit.
| n | Knight's Tour,
Using a Recursive Backtracking Search |
|---|
| | Class
Graph (file: graph.py) |
Knight's Tour
(file: knight.py) |
|---|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51 |
# graph.py: class giving adjacency list graph
import sys
class Graph(object):
def __init__(self):
self.__numV = 0 # num of vertices
self.__g = []
# insert/put stuff ###############
def insertVertex(self, d=None):
self.__numV += 1
self.__g.append([d, []])
def insertEdge(self, u, v, d=None):
self.__g[u][1].append([v,d]);
def putVertexData(self, v, d):
self.__g[v][0] = d
def putEdgeData(self, u, v, d):
# assumes unique edges
for w in self.__g[u][1]:
if w[0] == v:
w[1] = d
return
# get stuff ######################
def getNumV(self):
return self.__numV
def getVertexData(self, u):
return self.__g[u][0]
def getEdgeData(self, u, v):
for w in self.__g[u][1]:
if w[0] == v:
return w[1]
return None
def getAdjList(self, u, d):
ret = []
if u < 0 or u >= self.__numV:
return None
elif len(self.__g[u][1]) == 0:
return None
else:
t = len(self.__g[u][1])
for i in range(0,t):
if self._g[u][1][i][1] == d:
ret.append(self.\
__g[u][1][i][0])
return ret
# print stuff ####################
def printGraph(self):
sys.stdout.write("g = [\n")
for i in range(len(self.__g)):
sys.stdout.write(str(self.__g[i])
+ ", # " + str(i) + '\n')
sys.stdout.write("]\n")
| # knight0.py: backtracking search
import sys
from graph import *
N = 6 # size of chessboard
start = 0
# convert chess coordinates
def itot(i):
return (i//N, i%N)
def ttoi(t):
return t[0]*N + t[1]
k1, k2 = 1, 2 # knight moves
moves=[(k1,k2),(-k1,k2),(k1,-k2),(-k1,-k2),
(k2,k1),(-k2,k1),(k2,-k1),(-k2,-k1)]
# construct graph
g = Graph()
for i in range(N*N):
g.insertVertex(0) # 0 means color white
t = itot(i)
for j in range(8):
# try move j
s = moves[j]
if 0 <= (t[0]+s[0]) < N and\
0 <= (t[1]+s[1]) < N:
g.insertEdge(i,ttoi((t[0]+s[0],
t[1]+s[1])),None)
# carry out recursive backtracking search
st = []
def tour(u, pathlen):
st.append(u)
if pathlen > N*N - 2:
if st[N*N-1] == N+2 or \
st[N*N-1] == 2*N+1:
st.append(st[0])
sys.stdout.write("path: " +
str(st)+'\n')
g.putVertexData(u,1) # color is black
# each edge datum is None
for v in g.getAdjList(u, None):
if g.getVertexData(v) == 0: # white
# recursive call
tour(v, pathlen+1)
# returned somehow
# done with adj list
g.putVertexData(u, 0) # white, key step
st.pop() # also pop stack
tour(start, 0)
|
| n | Internal
form of Graph, many blanks deleted (file:
graph6)
|
|---|
g = [
[0,[[ 8,None],[13,None]]], # 0
[0,[[ 9,None],[14,None],[12,None]]], # 1
[0,[[10,None],[ 6,None],[15,None],[13,None]]], # 2
[0,[[11,None],[ 7,None],[16,None],[14,None]]], # 3
[0,[[ 8,None],[17,None],[15,None]]], # 4
[0,[[ 9,None],[16,None]]], # 5
[0,[[14,None],[ 2,None],[19,None]]], # 6
[0,[[15,None],[ 3,None],[20,None],[18,None]]], # 7
[0,[[16,None],[ 4,None],[12,None],[ 0,None],[21,None],[19,None]]], # 8
[0,[[17,None],[ 5,None],[13,None],[ 1,None],[22,None],[20,None]]], # 9
[0,[[14,None],[ 2,None],[23,None],[21,None]]], # 10
[0,[[15,None],[ 3,None],[22,None]]], # 11
[0,[[20,None],[ 8,None],[25,None],[ 1,None]]], # 12
[0,[[21,None],[ 9,None],[26,None],[ 2,None],[24,None],[ 0,None]]], # 13
[0,[[22,None],[10,None],[18,None],[ 6,None],[27,None],[ 3,None],[25,None],[1,None]]], # 14
[0,[[23,None],[11,None],[19,None],[ 7,None],[28,None],[ 4,None],[26,None],[2,None]]], # 15
[0,[[20,None],[ 8,None],[29,None],[ 5,None],[27,None],[ 3,None]]], # 16
[0,[[21,None],[ 9,None],[28,None],[ 4,None]]], # 17
[0,[[26,None],[14,None],[31,None],[ 7,None]]], # 18
[0,[[27,None],[15,None],[32,None],[ 8,None],[30,None],[ 6,None]]], # 19
[0,[[28,None],[16,None],[24,None],[12,None],[33,None],[ 9,None],[31,None],[7,None]]], # 20
[0,[[29,None],[17,None],[25,None],[13,None],[34,None],[10,None],[32,None],[8,None]]], # 21
[0,[[26,None],[14,None],[35,None],[11,None],[33,None],[ 9,None]]], # 22
[0,[[27,None],[15,None],[34,None],[10,None]]], # 23
[0,[[32,None],[20,None],[13,None]]], # 24
[0,[[33,None],[21,None],[14,None],[12,None]]], # 25
[0,[[34,None],[22,None],[30,None],[18,None],[15,None],[13,None]]], # 26
[0,[[35,None],[23,None],[31,None],[19,None],[16,None],[14,None]]], # 27
[0,[[32,None],[20,None],[17,None],[15,None]]], # 28
[0,[[33,None],[21,None],[16,None]]], # 29
[0,[[26,None],[19,None]]], # 30
[0,[[27,None],[20,None],[18,None]]], # 31
[0,[[28,None],[24,None],[21,None],[19,None]]], # 32
[0,[[29,None],[25,None],[22,None],[20,None]]], # 33
[0,[[26,None],[23,None],[21,None]]], # 34
[0,[[27,None],[22,None]]], # 35
]| Sample Output
Tour
|
|---|
[ 0, 8, 16, 5, 9, 1, 14, 3, 11, 22, 35, 27, 31, 18, 7, 15, 4, 17, 28, 32,
24, 20, 12, 25, 33, 29, 21, 34, 23, 10, 2, 6, 19, 30, 26, 13, 0]
| |
Notice that the "internal form" above could be used as an assignment
inside a program to define this graph. It would be better to use
json to input it, but I haven't gotten that to work yet.
The final trailing comma inside the list at the top level makes no
difference -- it doesn't change the length of the list.
In the specific search above, the program got off to a bad search start,
first going to 8 and then a bit later to 13, so it was
impossible to finish a tour until it had backtracked past the 13.
It labored for hours (and almost a billion knight moves) before coming up with
hundreds of tours.
Given this difficulty with N = 6, the case N = 8 is already not
feasible using this approach.
A Heuristic to
Improve the Search: In the online course:
Problem Solving with Algorithms and Data Structures,
the section:
Knight's Tour Analysis suggests choosing each knight move
to the square with the least number of possible further moves.
| n | Knight's Tour,
Using a Recursive Backtracking Search |
|---|
| |
Knight's Tour
(file: knight.py) |
|---|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
# knight.py: heuristic search
import sys
from graph import *
if len(sys.argv) != 2:
sys.stdout.write("Usage: ")
sys.stdout.write("python knight.py 6\n")
sys.exit()
N = int(sys.argv[1]) # size of chessboard
start = N + 2
# convert chess coordinates
def itot(i):
return (i//N, i%N)
def ttoi(t):
return t[0]*N + t[1]
k1, k2 = 1, 2 # knight moves
moves=[(k1,k2),(-k1,k2),(k1,-k2),(-k1,-k2),
(k2,k1),(-k2,k1),(k2,-k1),(-k2,-k1)]
# stuff related to reordering adj lists
def entries(i, j):
e = []
for k in range(8):
s = moves[k]
if 0 <= i + s[0] < N and\
0 <= j + s[1] < N:
e.append(ttoi([i+s[0], j+s[1]]))
return e
| # create graph
g = Graph()
for i in range(N*N):
g.insertVertex(0) # 0 is color white
t = itot(i)
for j in range(8):
# try move j
s = moves[j]
if 0 <= (t[0]+s[0]) < N and\
0 <= (t[1]+s[1]) < N:
g.insertEdge(i,ttoi((t[0]+s[0],
t[1]+s[1])),None)
# carry out recursive backtracking search
st = []
def tour(u, pathlen):
st.append(u)
if pathlen > N*N - 2:
if st[N*N-1] in entries(start//N,
start%N):
st.append(st[0])
sys.stdout.write("path: " +
str(st)+'\n')
sys.exit()
g.putVertexData(u,1) # color is black
# first reorder the adj list
adj = g.getAdjList(u, None)
adj.sort(key=lambda x: \
len(entries(x//N,x%N)))
# each edge datum is None
for v in adj:
if g.getVertexData(v) == 0: # white
# recursive call
tour(v, pathlen+1)
# returned somehow
# done with adj list
g.putVertexData(u, 0) # white, key step
st.pop() # also pop stack
tour(start, 0)
|
| Output |
|---|
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
% python knight.py 6
[ 8, 0, 13, 24, 32, 28, 17, 4, 15, 11, 3, 7, 18, 31, 27, 35, 22, 33, 29, 21,
25, 12, 20, 16, 5, 9, 1, 14, 6, 2, 10, 23, 34, 26, 30, 19, 8]
% python knight.py 8
[10, 0, 17, 2, 8, 25, 40, 57, 51, 61, 55, 38, 23, 6, 12, 22, 7, 13, 3, 9,
24, 41, 56, 50, 60, 54, 39, 45, 62, 47, 53, 63, 46, 31, 14, 4, 21, 15, 5, 11,
1, 16, 33, 48, 58, 52, 42, 32, 49, 59, 44, 34, 28, 18, 35, 29, 19, 36, 30, 20,
26, 43, 37, 27, 10]
% python knight.py 10
[12, 0, 21, 2, 10, 31, 50, 71, 90, 82, 94, 86, 98, 79, 87, 99, 78, 59, 38, 19,
7, 15, 3, 11, 30, 51, 70, 91, 83, 95, 76, 88, 96, 84, 92, 80, 61, 40, 52, 60,
81, 93, 85, 97, 89, 68, 49, 28, 9, 17, 29, 8, 16, 4, 25, 6, 18, 39, 58, 66,
74, 62, 41, 20, 1, 13, 5, 26, 14, 22, 34, 46, 54, 73, 65, 77, 69, 57, 36, 44,
23, 42, 63, 75, 67, 48, 27, 35, 47, 55, 43, 24, 32, 53, 72, 64, 56, 37, 45, 33,
12]
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
|
The main implementation problem was to sort each adjacency list
in order of increasing number of possible next moves (least number of
possibilities first). The program uses a function entries which
returns the possible next moves as a list. Then the adjacency list,
called adj, is sorted using the method sort, and
the length of the number of possible moves as the key.
This kind of sort is more frequently used in an example such as the
one below, where one wants to ignore case when sorting strings.
The only advantage of the lambda below is to shorten
the code and to avoid another function name.
| Use of sort method |
|---|
import sys
a = ['Neal', 'ned', 'joe', 'James', 'Ted', 'shaw', 'Shaw', ]
b = a
c = a
a.sort() # normal in-place sort
sys.stdout.write(str(a) + '\n')
b.sort(key = lambda n: n.lower()) # using lambda function
sys.stdout.write(str(b) + '\n')
def low(x):
return x.lower()
c.sort(key = low) # using separate function
sys.stdout.write(str(c) + '\n')
% python test_sort2.py
['James', 'Neal', 'Shaw', 'Ted', 'joe', 'ned', 'shaw']
['James', 'joe', 'Neal', 'ned', 'Shaw', 'shaw', 'Ted']
['James', 'joe', 'Neal', 'ned', 'Shaw', 'shaw', 'Ted']
|
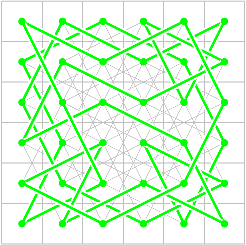
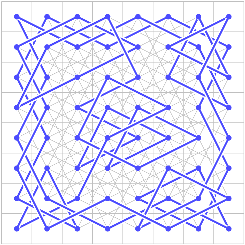
Here are pictures of three results of the heuristic technique above
for sizes 6, 8, and 10, starting in each case
so that the next move goes to square 0.
The picture uses Postscript as described in the next section.
Because of the heuristic, the first two each finished in less
than a second. Even with the heuristic, the third one took several
hours.
Postscript
Pictures of Tours: I use several programs to generate
a Postscript program that will illustrate a given knight's path.
- The blue parts of the program above
generate most of the blue code below (except for a little
at the beginning and the end). This code directly draws 362
lines that are the edges of the graph for the knight moves.
The code is contained in the
file: knight6.init.txt.
- I wrote the red code in the program below
by hand. This code draws the 36 vertices (Postscript
function circles); it draws
the chessboard "grid" (Postscript function grid); and it
draws each individual line of the path (Postscript function
xlineto). This last draws each path segment as a wide
white line with a narrower red line overwriting it.
The code is contained in the
file: knight6.term.txt.
- The black code in the program above is generated from
the sequence of vertices in the path or tour, using the program at
the bottom below.
| Knight's Tour,
Generate Postscript Picture (file:
path6.ps) |
|---|
%!PS-Adobe-2.0
/Black{0 0 0 1 setcmykcolor} def
/White{0 0 0 0 setcmykcolor} def
/Gray{0 0 0 0.25 setcmykcolor} def
/Green{1 0 1 0 setcmykcolor} def
/Red{0 1 1 0 setcmykcolor} def
/N 6 def
/moves {
0 0 moveto 1 2 lineto stroke 0 0 moveto 2 1 lineto stroke
0 1 moveto 1 3 lineto stroke 0 1 moveto 2 2 lineto stroke
0 1 moveto 2 0 lineto stroke 0 2 moveto 1 4 lineto stroke
0 2 moveto 1 0 lineto stroke 0 2 moveto 2 3 lineto stroke
0 2 moveto 2 1 lineto stroke 0 3 moveto 1 5 lineto stroke
0 3 moveto 1 1 lineto stroke 0 3 moveto 2 4 lineto stroke
0 3 moveto 2 2 lineto stroke 0 4 moveto 1 2 lineto stroke
0 4 moveto 2 5 lineto stroke 0 4 moveto 2 3 lineto stroke
0 5 moveto 1 3 lineto stroke 0 5 moveto 2 4 lineto stroke
1 0 moveto 2 2 lineto stroke 1 0 moveto 0 2 lineto stroke
1 0 moveto 3 1 lineto stroke 1 1 moveto 2 3 lineto stroke
1 1 moveto 0 3 lineto stroke 1 1 moveto 3 2 lineto stroke
1 1 moveto 3 0 lineto stroke 1 2 moveto 2 4 lineto stroke
1 2 moveto 0 4 lineto stroke 1 2 moveto 2 0 lineto stroke
1 2 moveto 0 0 lineto stroke 1 2 moveto 3 3 lineto stroke
1 2 moveto 3 1 lineto stroke 1 3 moveto 2 5 lineto stroke
1 3 moveto 0 5 lineto stroke 1 3 moveto 2 1 lineto stroke
1 3 moveto 0 1 lineto stroke 1 3 moveto 3 4 lineto stroke
1 3 moveto 3 2 lineto stroke 1 4 moveto 2 2 lineto stroke
1 4 moveto 0 2 lineto stroke 1 4 moveto 3 5 lineto stroke
1 4 moveto 3 3 lineto stroke 1 5 moveto 2 3 lineto stroke
1 5 moveto 0 3 lineto stroke 1 5 moveto 3 4 lineto stroke
2 0 moveto 3 2 lineto stroke 2 0 moveto 1 2 lineto stroke
2 0 moveto 4 1 lineto stroke 2 0 moveto 0 1 lineto stroke
2 1 moveto 3 3 lineto stroke 2 1 moveto 1 3 lineto stroke
2 1 moveto 4 2 lineto stroke 2 1 moveto 0 2 lineto stroke
2 1 moveto 4 0 lineto stroke 2 1 moveto 0 0 lineto stroke
2 2 moveto 3 4 lineto stroke 2 2 moveto 1 4 lineto stroke
2 2 moveto 3 0 lineto stroke 2 2 moveto 1 0 lineto stroke
2 2 moveto 4 3 lineto stroke 2 2 moveto 0 3 lineto stroke
2 2 moveto 4 1 lineto stroke 2 2 moveto 0 1 lineto stroke
2 3 moveto 3 5 lineto stroke 2 3 moveto 1 5 lineto stroke
2 3 moveto 3 1 lineto stroke 2 3 moveto 1 1 lineto stroke
2 3 moveto 4 4 lineto stroke 2 3 moveto 0 4 lineto stroke
2 3 moveto 4 2 lineto stroke 2 3 moveto 0 2 lineto stroke
2 4 moveto 3 2 lineto stroke 2 4 moveto 1 2 lineto stroke
2 4 moveto 4 5 lineto stroke 2 4 moveto 0 5 lineto stroke
2 4 moveto 4 3 lineto stroke 2 4 moveto 0 3 lineto stroke
2 5 moveto 3 3 lineto stroke 2 5 moveto 1 3 lineto stroke
2 5 moveto 4 4 lineto stroke 2 5 moveto 0 4 lineto stroke
3 0 moveto 4 2 lineto stroke 3 0 moveto 2 2 lineto stroke
3 0 moveto 5 1 lineto stroke 3 0 moveto 1 1 lineto stroke
3 1 moveto 4 3 lineto stroke 3 1 moveto 2 3 lineto stroke
3 1 moveto 5 2 lineto stroke 3 1 moveto 1 2 lineto stroke
3 1 moveto 5 0 lineto stroke 3 1 moveto 1 0 lineto stroke
3 2 moveto 4 4 lineto stroke 3 2 moveto 2 4 lineto stroke
3 2 moveto 4 0 lineto stroke 3 2 moveto 2 0 lineto stroke
3 2 moveto 5 3 lineto stroke 3 2 moveto 1 3 lineto stroke
3 2 moveto 5 1 lineto stroke 3 2 moveto 1 1 lineto stroke
3 3 moveto 4 5 lineto stroke 3 3 moveto 2 5 lineto stroke
3 3 moveto 4 1 lineto stroke 3 3 moveto 2 1 lineto stroke
3 3 moveto 5 4 lineto stroke 3 3 moveto 1 4 lineto stroke
3 3 moveto 5 2 lineto stroke 3 3 moveto 1 2 lineto stroke
3 4 moveto 4 2 lineto stroke 3 4 moveto 2 2 lineto stroke
3 4 moveto 5 5 lineto stroke 3 4 moveto 1 5 lineto stroke
3 4 moveto 5 3 lineto stroke 3 4 moveto 1 3 lineto stroke
3 5 moveto 4 3 lineto stroke 3 5 moveto 2 3 lineto stroke
3 5 moveto 5 4 lineto stroke 3 5 moveto 1 4 lineto stroke
4 0 moveto 5 2 lineto stroke 4 0 moveto 3 2 lineto stroke
4 0 moveto 2 1 lineto stroke 4 1 moveto 5 3 lineto stroke
4 1 moveto 3 3 lineto stroke 4 1 moveto 2 2 lineto stroke
4 1 moveto 2 0 lineto stroke 4 2 moveto 5 4 lineto stroke
4 2 moveto 3 4 lineto stroke 4 2 moveto 5 0 lineto stroke
4 2 moveto 3 0 lineto stroke 4 2 moveto 2 3 lineto stroke
4 2 moveto 2 1 lineto stroke 4 3 moveto 5 5 lineto stroke
4 3 moveto 3 5 lineto stroke 4 3 moveto 5 1 lineto stroke
4 3 moveto 3 1 lineto stroke 4 3 moveto 2 4 lineto stroke
4 3 moveto 2 2 lineto stroke 4 4 moveto 5 2 lineto stroke
4 4 moveto 3 2 lineto stroke 4 4 moveto 2 5 lineto stroke
4 4 moveto 2 3 lineto stroke 4 5 moveto 5 3 lineto stroke
4 5 moveto 3 3 lineto stroke 4 5 moveto 2 4 lineto stroke
5 0 moveto 4 2 lineto stroke 5 0 moveto 3 1 lineto stroke
5 1 moveto 4 3 lineto stroke 5 1 moveto 3 2 lineto stroke
5 1 moveto 3 0 lineto stroke 5 2 moveto 4 4 lineto stroke
5 2 moveto 4 0 lineto stroke 5 2 moveto 3 3 lineto stroke
5 2 moveto 3 1 lineto stroke 5 3 moveto 4 5 lineto stroke
5 3 moveto 4 1 lineto stroke 5 3 moveto 3 4 lineto stroke
5 3 moveto 3 2 lineto stroke 5 4 moveto 4 2 lineto stroke
5 4 moveto 3 5 lineto stroke 5 4 moveto 3 3 lineto stroke
5 5 moveto 4 3 lineto stroke 5 5 moveto 3 4 lineto stroke
} def
|
/path {
5 2 3 3 xlineto
3 3 5 4 xlineto
5 4 3 5 xlineto
3 5 1 4 xlineto
1 4 0 2 xlineto
0 2 1 0 xlineto
1 0 2 2 xlineto
2 2 0 1 xlineto
0 1 2 0 xlineto
2 0 4 1 xlineto
4 1 5 3 xlineto
5 3 4 5 xlineto
4 5 2 4 xlineto
2 4 0 5 xlineto
0 5 1 3 xlineto
1 3 3 4 xlineto
3 4 4 2 xlineto
4 2 5 0 xlineto
5 0 3 1 xlineto
3 1 1 2 xlineto
1 2 0 0 xlineto
0 0 2 1 xlineto
2 1 4 0 xlineto
4 0 3 2 xlineto
3 2 4 4 xlineto
4 4 2 5 xlineto
2 5 0 4 xlineto
0 4 2 3 xlineto
2 3 1 5 xlineto
1 5 0 3 xlineto
0 3 1 1 xlineto
1 1 3 0 xlineto
3 0 5 1 xlineto
5 1 4 3 xlineto
4 3 5 5 xlineto
} def
/xlineto {
/y2 exch def
/x2 exch def
/y1 exch def
/x1 exch def
gsave
0.15 setlinewidth White
x1 y1 moveto
x2 y2 lineto stroke
grestore
0.06 setlinewidth
x1 y1 moveto
x2 y2 lineto stroke
} def
/circles {
0 1 N 1 sub {
/xloc exch def
0 1 N 1 sub {
/yloc exch def
xloc yloc 0.09
0 360 arc fill
} for
} for
} def
/grid {
0 1 N {
/xloc exch def
-0.5 xloc add -0.5 moveto
-0.5 xloc add
N .5 sub lineto
stroke
} for
0 1 N {
/yloc exch def
-0.5 -0.5 yloc add moveto
N .5 sub -0.5
yloc add lineto
stroke
} for
} def
150 200 translate
60 60 scale
0.02 setlinewidth
Gray grid
0.01 setlinewidth
Gray moves
0.04 setlinewidth
Green path
Green circles
showpage
|
Generate
Postscript Code to
to Generate Postscript Picture
(file: path6.py) |
|---|
# path6.py: get postscript picture of path
import sys
fout = open("path6.ps",'w')
def genf(infile): # output Postscript files
f = open(infile, 'r')
for line in f:
fout.write(line)
N = 6
def itot(i):
return (i//N, i%N)
def ttoi(t):
return t[0]*N + t[1]
# successive vertices in a path
tour = [17, 21, 29, 33, 25, 12, 1, 14,
6, 2, 10, 23, 34, 26, 30, 19,
27, 16, 5, 9, 13, 0, 8, 4,
15, 28, 32, 24, 20, 31, 18, 7,
3, 11, 22, 35]
genf("path6.init.txt")
# write ps code for path edges
for i in range(len(tour)-1):
(t1, t2) = itot(tour[i])
(t3, t4) = itot(tour[i+1])
fout.write(str(t2)+" "+str(t1)+" "+
str(t4)+" "+str(t3)+" xlineto\n")
genf("path6.term.txt")
|
|
Result of
path6.ps
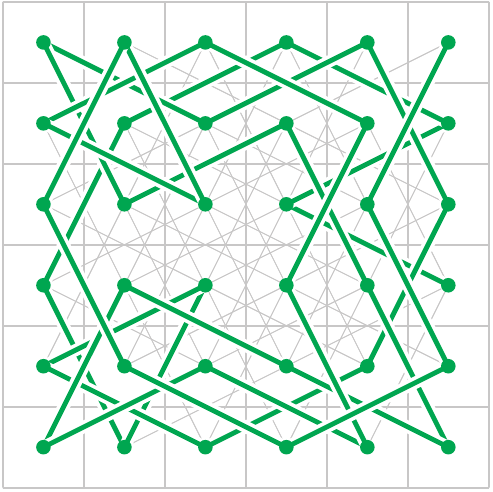
.pdf
|
Constructing
Tours:
|
It's clear above that straightforward search is too inefficient
to generate knight's tours in a reasonable amount of time even
for N = 6. There is a tremendous amount of information
about creating tours more efficiently. For example,
see The Knight's Tour
for many complex constructions, including the two at the right.
|

|
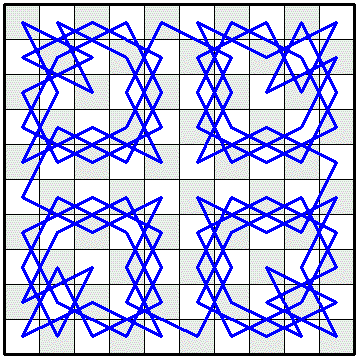 |
(Revision date: 2015-04-14.
Please use ISO 8601,
the International Standard.)
|