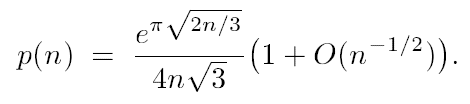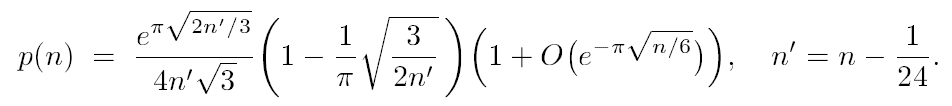| |
 |
|
Python |
14. Counting Partitions
|
|
Counting Partitions:
See
partition function from Wikipedia for a definition
of partition.
Here is a recurrence equation for the nth partition
(discovered by the Swiss mathematician Euler):
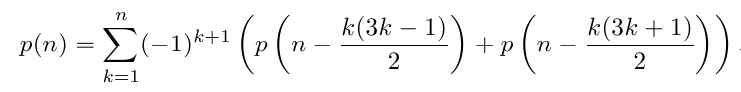 , ,
where p(0) = 1 and p(n) = 0 for all n < 0.
(Initially I didn't realize that the above formula generates
a huge number of negative calls to p, and these caused debugging
problems. All such calls should return 0.)
|
Counting Partitions |
|---|
| Program |
"Memoized" (in red) |
|---|
# part.py: recursive relation
import sys
LIM = 40
def p(n):
if n < 0:
return 0
if n == 0: # or n == 1 speeds up
return 1
# print "Call p with n = %i" % n
sign = 1
res = 0
for k in range(1, n+1):
term = p(n - k*(3*k - 1)/2)+\
p(n - k*(3*k + 1)/2)
res = res + sign*term
sign = -sign
return res
n = 0
while n <= LIM:
res = p(n)
print n, res
n = n+1
print "\n"
| # part.py: memoized version
import sys
LIM = 10000
pmem = [0.0]*(LIM+1)
def insertp(t, loc):
pmem[loc] = t
def p(n):
if n < 0:
return 0
if n == 0:
return 1
if pmem[n] != 0:
return pmem[n]
sign = 1
res = 0
for k in range(1, n+1):
p1 = n - k*(3*k - 1)/2
if p1 >= 0:
term1 = p(p1)
insertp(term1, p1)
else:
term1 = 0
p2 = n - k*(3*k + 1)/2
if p2 >= 0:
term2 = p(p2)
insertp(term2, p2)
else:
term2 = 0
term = term1 + term2
res = res + sign*term
sign = -sign
return res
print "LIM:", LIM
n = 0
while n <= LIM:
res = p(n)
if n%100 == 0:
print n, res
n = n+1
print "\n"
|
The Python program on the left works but is impossibly slow.
It slows a program to a crawl well before n = 30, while
a C version slows before 40. The Python memoized version
computed p(1000) in a few seconds. The memoizing features
are shown in red. The answer agreed with
the cited correct value. See
Decorators for the use of decorators in memoization.
p(1000) = 24061467864032622473692149727991
|
Python Recursion Limit:
Suppose one replaces the last 7 lines above on the right with just:
print p(LIM)
Then the calculation works well and quickly for
LIM < 998
but it fails with the message
"RuntimeError: maximum recursion depth exceeded in cmp" for
LIM > 999
Online, during a simple discussion of using tail recursion, one
contributor wrote:
[The default recursion limit] is a guard against a stack overflow, [and]
yes. Python (or rather, the CPython implementation) doesn't optimize
tail recursion, and unbridled recursion causes stack overflows.
You can change the recursion limit with sys.setrecursionlimit(),
but doing so is dangerous -- the standard limit is a little
conservative, but Python stackframes can be quite big.
Python isn't a functional language and tail recursion is not
a particularly efficient technique. Rewriting the algorithm
iteratively, if possible, is generally a better idea.
In the case above, eliminating recursion would be annoying
(at least for me), but the memoization works fine. It's interesting
that even with memoization, it's necessary to compute the
numbers explicitly in increasing order.
If I use
LIM = 1500
in the program, and include
sys.setrecursionlimit(1502)
print sys.getrecursionlimit()
the program completes (on my very slow PC) in about 3 seconds
with the correct answer.
Using
LIM = sys.setrecursionlimit(1501)
it fails as above.
Output for LIM = 10000:
The program on the right above prints every 100th value of n.
|

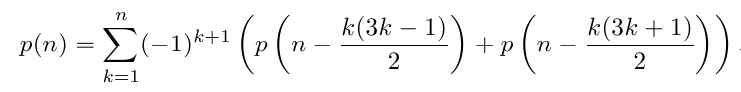 ,
,