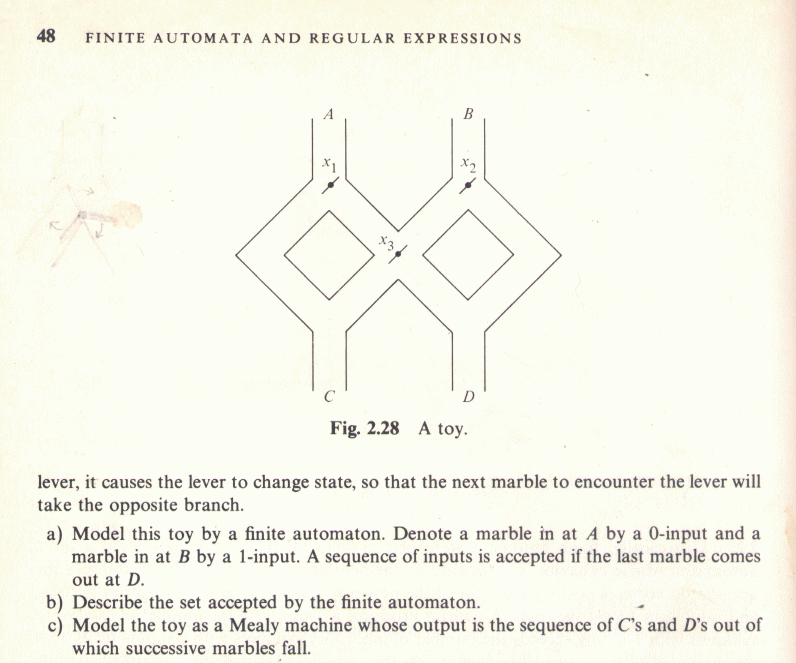
Rotor
Puzzle |
 |
As shown above, the rotor puzzle is made up of six triangular pieces, where each piece has a fixed portion and a ``rotor'' that turns. These six triangular pieces are locked together, but the whole puzzle can be oriented in any of the six positions with a flat portion above and below.
In each orientation, a cylindrical ``roller'' is inserted into one of the three upper holes. As the roller goes downward, it turns the rotors by 60 or 120 degrees. The roller comes out one of the three lower holes, depending on the positions of the rotors. Insert the roller again, and it will take a different path because 2, 3, or 4 of the rotors have changed position. The object is to get all rotors pointing in the same direction. The white dot at the end of one arm of each rotor keeps track of the rotor's position. The rotors are constructed so that they don't spin freely, but tend to ``stick'' in one of the six orientations shown below. The weight of the roller is just enough to push the rotors around.
The normal 6-rotor puzzle is made up from six identical triangular parts as shown above. Each part has one rotor with three arms sticking out, rotating around the black dot in the center. There are three holes on the three sides of the triangle, just the size to admit the roller. Six of these parts are connected together (hole-to-hole) in the two orientations shown below, three in the first orientation and three in the second.
 |
 |
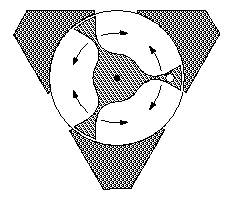
The illustration below shows the first orientation. Here the roller enters the top hole and exits one of the two bottom holes, depending on the orientation of the rotor. The figures show three successive stages, with roller positions numbered 1, 2, and 3. In this case the roller exits through the righthand hole. The rotor turns clockwise by 60 degrees as the roller passes through, and the rotor sticks in that new position. If the roller were inserted again, it would turn the rotor 60 degrees counter-clockwise and exit at the left. This part of the puzzle would then be back the way it was before inserting the roller twice.
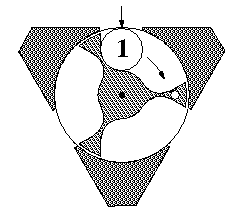 |
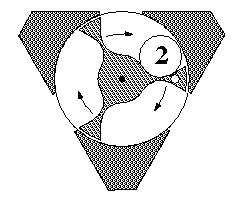 |
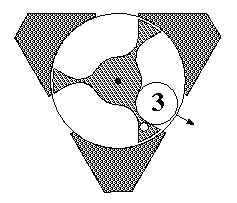 |
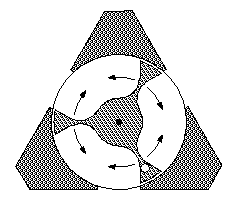
The next illustration below shows the second orientation. The roller enters either of the two top holes and always exits the bottom hole. Again the figures show three successive stages, using ball positions numbered 1, 2, and 3, where the roller is inserted at the right. In this case the rotor rotates clockwise 60 degrees. If the rotor were in the other postion (60 degrees from what is shown), the rotor would rotate clockwise 120 degrees as the roller goes through. Inserting the roller at the left results in counter-clockwise rotations of 60 or 120 degrees.
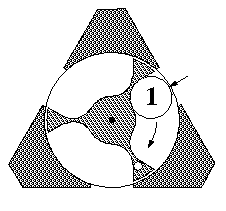 |
 |
 |
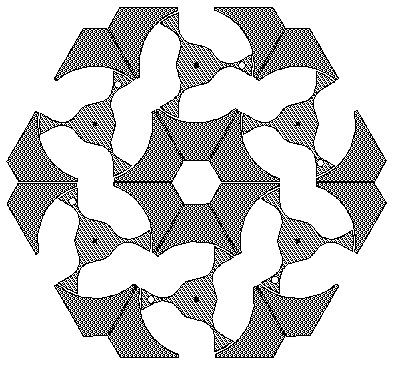
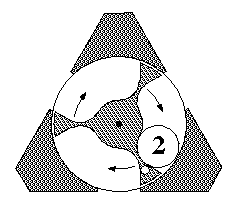
The next diagram shows a hexagonal puzzle configuration with six parts. The roller can be inserted in any of the top three holes. It will exit from one of the bottom three holes, depending on the rotor positions. After exiting, either 2, 3, or 4 rotors will be rotated from their previous positions. The whole puzzle can be rotated into any of six positions before each insertion of the roller. This illustration shows black dots for the centers of rotation.
If one inserted the roller in the center top hole, it would go right, rotating the top rotor 60 degrees clockwise, then down, rotating the upper right rotor 120 degrees counter-clockwise, and finally it would exit from the lower right triangle, having rotated the lower right rotor by 60 degrees clockwise. If one inserted the roller again in the center top hole, it would go to the left this second time, and would pass through 4 triangles. After two roller insertions at the top, the top rotor would be back where it started, while all other rotors would have rotated once each.
 |
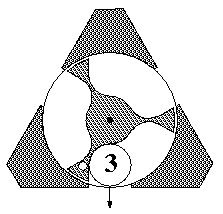
The actual puzzle is missing the black dots. The puzzle also has a picture of a large rotor (three times as large) painted on the front, with a large white dot to show the whole puzzle's orientation. This configuration looks like the illustrations on the page before following the link to this page.
Finally, in the actual puzzle, the roller itself has another picture of a rotor on it, a third the size of the actual rotors. The puzzle has a transparent cover on the front side so that you can see the rotors. The objective of the puzzle is to achieve a final position of rotors with all of them pointing the same way as the large painted rotor.
One can also combine more than six triangular parts to make up other more complicated configurations.
Postscript Illustrations:
Here is code in the Postscript language to generate the figure on the page before this one:Postscript Code. Exactly this code will produce the figure shown if it is sent to a Postscript printer.
Simulation in C:
Here is a portion of a C program that will simulate the puzzle: Partial C Simulation Program. Here is complete C simulation program (used to simulate the case below that limits the roller entry to straight down): Complete C Simulation Program.
There are 66 = 46656 different configurations of the basic 6-rotor puzzle, according to the 6 possible positions of each of the 6 rotors. (The whole puzzle can be rotated with any of 6 possible sides up, but such rotations do not yield different configurations.)
One possible way to play a game based on the puzzle is to try to reach a given configuration from an all-lined-up configuration. Of the 46656 possibilities, only 15552 are reachable from a lined-up configuration by repeatedly inserting the roller into one of the three upper holes and by rotating the puzzle. All 15552 can be reached in at most 10 insertions, though that is based on a computer search and would be hard to discover by hand. As a puzzle, one could "mess it up" by using the roller at random, and then ask someone to restore it to the lined-up form.
Another possible game is to limit insertion to the upper middle hole, not allowing the side holes, but allowing whole puzzle to be rotated in any of the six ways. With this limitation it would be harder to effect changes in the rotors. In this case there are 13608 configurations reachable from an all-lined-up configuration. Here again each can be reached in 10 or fewer insertions.
Addendum:
I created this puzzle after a long period of thinking about the following exercise, taken from the book Introduction to Automata Theory, Languages, and Computation, by J.E. Hopcroft and J.D. Ullman, Addison-Wesley, 1979, pages 47-48, Problem 2.3. (There is now a third edition, but this first edition is the "clasic" that some people prefer.)
I started out trying to create a version of their toy that would function with real marbles, but I turned to generalizing and regularizing it, eventually hitting on my "rotor" that works in any one of six orientations. Here are scanned images that give Problem 2.3.