Here are the 29 pentacubes:

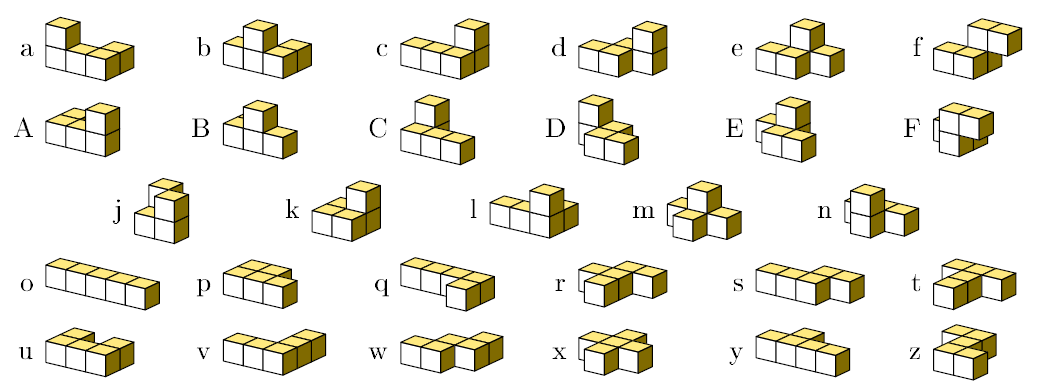In 1972 I published two articles showing constructions using these pentacubes.

In early 2017, Donald Knuth gave an astonishing construction using all 29 pieces. The material below comes from Donald Knuth's The Art of Computer Programming, Vol.4, 7.2.2.1. Dancing Links, which he also calls Pre-Fascicle 5C or just Fasc5C. (This is a work in progress.)

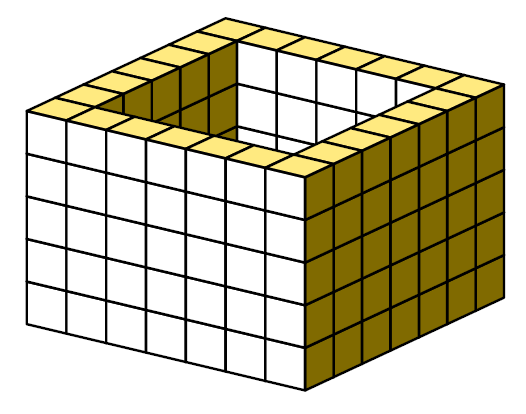
In Problem 221 of his Fasc5C Knuth writes: "221. [25] The full set of 29 pentacubes can build an enormous variety of elegant structures, including a particularly stunning example called 'Dowler's Box.' This 7 x 7 x 5 container, first considered by R.W.M. Dowler in 1979, is constructed from five flat slaps. Yet only 12 of the pentacubes lie flat; the other 17 must somehow be worked into the edges and corners.         Despite these difficulties, Dowler's Box has so many solutions that we can actually impose many further conditions on its construction:               [Skipping conditions (a) and (b) of the problem.]         c) Alternatively, place piece x in the center, and build the remaining structure from four congruent pieces that have seven pentacubes each."

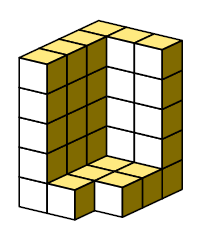
Here is Knuth's partial "answer" to this problem: "221. (c) This computation, due to Torsten Sillke [see Cubism For Fun 27 (1991), 15], goes much faster: The quarter-of-a-box shown here can be packed with seven non-x pentacubes in 55356 ways, found in 1.3 Gμ. As in answer 177, this yields a new exact cover problem, with 33412 different rows. Then 11.8 Gμ more computation discovers seven suitable partitions into four sets of seven, one of which is illustrated here."

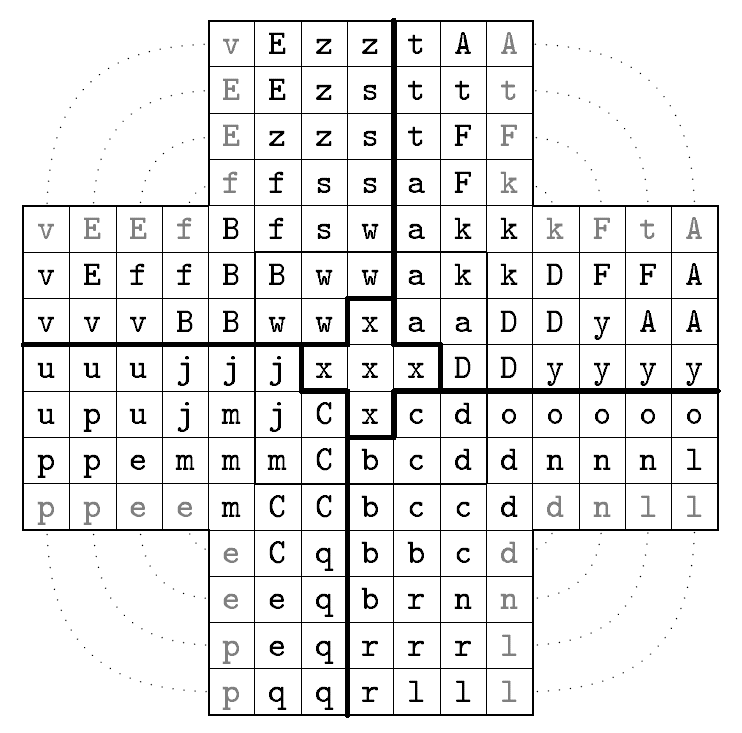In the diagram above, the four 7-by-4 rectangles are each stacked above the inner 7-by-7 square. Dark-lettered cubes occur only once, but light-lettered cubes are paired up along the dotted lines.

Below is Dowler's box constructed from my set of wooden pentacubes. On the left is the box itself, and the other two pictures give two views of this version of the box pulled into its 5 components.