 |
CS 3723 Programming Languages |
Tiny® Test Programs (with doubles) | |
Tiny® Sample 6: First is a program to calculate π. The Tiny code uses Newton's method to calculate the square root.
| Tiny Program | Equivalent C Program | Common Output |
|---|---|---|
| Sample 6: Using Product Formula (below) to Calculate π | ||
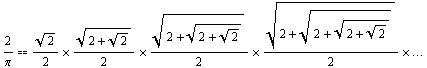 |
# trans pi2.t to pi2.s % spim pi2.s 26 2 2.828427124746190 3 3.061467458920718 4 3.121445152258052 5 3.136548490545939 6 3.140331156954753 7 3.141277250932773 8 3.141513801144301 9 3.141572940367092 10 3.141587725277160 11 3.141591421511200 12 3.141592345570118 13 3.141592576584873 14 3.141592634338564 15 3.141592648776987 16 3.141592652386592 17 3.141592653288994 18 3.141592653514594 19 3.141592653570994 20 3.141592653585095 21 3.141592653588619 22 3.141592653589500 23 3.141592653589721 24 3.141592653589776 25 3.141592653589790 26 3.141592653589793 | |
# pi2.t: pi as product
> n;
p = 2; # final product
b = 0; # each denom
i = 1; # loop count
{ n - i ?
# b=sqrt(2+b), Newt #
k = 1; #
x = 2 + b; #
y = x; #
{ k - 2*5 ? #
y = x/(2*y)+y/2;#
k = k + 1; } #
b = y; #
# sqrt done #########
t = 2/b; # term
p = p*t;
i = i + 1;
< i; < B; < p; < N;
} $
|
// pi2.c: pi at a product
#include <stdio.h>
#include <math.h>
int main() {
double p, b, i, n, t;
scanf("%lf", &n);
p = 2; // final product
b = 0; // each denom
i = 1; // loop count
while (n - i != 0) {
b = sqrt(2 + b);
t = 2/b; // term
p = p*t;
i = i + 1;
printf("%.0f %.15f\n", i, p);
}
}
| |
Tiny® Sample 7: Next is a program to find prime factors of successive Fibonacci numbers:
| Sample 7: Successive Fibonacci Numbers and Their Prime Factorization | ||
|---|---|---|
| Tiny Program | Equivalent C Program | |
# fib.t: Fibonacci numbers
# and prime factorizations
f = 1; g = 2; n = 3;
> m;
{ m - n ?
< n; < T; < g; < T;
j = g; d = 2; t = 1;
{ t ?
[ j%d ? e = 0; : e = 1; ]
{ e ?
j = j/d;
< d; < B;
[ j%d ? e = 0; : e = 1; ]
}
[ j - 1 ? t = 1; : t = 0; ]
[ d - 2 ? d = d + 2; : d = 3; ]
}
< N;
n = n + 1;
h = f + g;
f = g; g = h;
} $
|
#include <stdio.h>
#include <math.h>
int main() {
double f, g, n, m, j, d, t, e, h;
f = 1; g = 2; n = 3;
scanf("%lf", &m);
while (m - n != 0) {
printf("%.0f\t%.0f\t", n, g);
j = g; d = 2; t = 1;
while (t != 0) {
if (fmod(j,d) != 0) e = 0; else e = 1;
while (e != 0) {
j = j/d;
printf("%.0f ", d);
if (fmod(j,d) != 0) e = 0; else e = 1;
}
if (j - 1 != 0) t = 1; else t = 0;
if (d - 2 != 0) d = d + 2; else d = 3;
}
printf("\n");
n = n + 1;
h = f + g;
f = g; g = h;
}
}
| |
| Common Output (SPIM is too slow for 43 and 47, and won't work at 48 on) | ||
# trans fib.t to fib.s % spim fib.s 71 3 2 2 4 3 3 5 5 5 6 8 2 2 2 7 13 13 8 21 3 7 9 34 2 17 10 55 5 11 11 89 89 12 144 2 2 2 2 3 3 13 233 233 14 377 13 29 15 610 2 5 61 16 987 3 7 47 17 1597 1597 18 2584 2 2 2 17 19 19 4181 37 113 20 6765 3 5 11 41 21 10946 2 13 421 22 17711 89 199 23 28657 28657 24 46368 2 2 2 2 2 3 3 7 23 25 75025 5 5 3001 26 121393 233 521 27 196418 2 17 53 109 28 317811 3 13 29 281 29 514229 514229 30 832040 2 2 2 5 11 31 61 31 1346269 557 2417 32 2178309 3 7 47 2207 33 3524578 2 89 19801 34 5702887 1597 3571 35 9227465 5 13 141961 | 36 14930352 2 2 2 2 3 3 3 17 19 107 37 24157817 73 149 2221 38 39088169 37 113 9349 39 63245986 2 233 135721 40 102334155 3 5 7 11 41 2161 41 165580141 2789 59369 42 267914296 2 2 2 13 29 211 421 43 433494437 433494437 44 701408733 3 43 89 199 307 45 1134903170 2 5 17 61 109441 46 1836311903 139 461 28657 47 2971215073 2971215073 48 4807526976 2 2 2 2 2 2 3 3 7 23 47 1103 49 7778742049 13 97 6168709 50 12586269025 5 5 11 101 151 3001 51 20365011074 2 1597 6376021 52 32951280099 3 233 521 90481 53 53316291173 953 55945741 54 86267571272 2 2 2 17 19 53 109 5779 55 139583862445 5 89 661 474541 56 225851433717 3 7 7 13 29 281 14503 57 365435296162 2 37 113 797 54833 58 591286729879 59 19489 514229 59 956722026041 353 2710260697 60 1548008755920 2 2 2 2 3 3 5 11 31 41 61 2521 61 2504730781961 4513 555003497 62 4052739537881 557 2417 3010349 63 6557470319842 2 13 17 421 35239681 64 10610209857723 3 7 47 1087 2207 4481 65 17167680177565 5 233 14736206161 66 27777890035288 2 2 2 89 199 9901 19801 67 44945570212853 269 116849 1429913 68 72723460248141 3 67 1597 3571 63443 69 117669030460994 2 137 829 18077 28657 70 190392490709135 5 11 13 29 71 911 141961 | |
Revision date: 2014-01-29. (Please use ISO 8601, the International Standard.)