CS 3721
Programming Languages  
Spring 2014
 Recitation 5.   Assignments 
Week 5: Feb 11 - 13

Submit following directions at: submissions and rules at: rules. Deadlines are:
  • 2014-02-18  23:59:59 (that's Tue,   18 Feb 2014, 11:59:59 pm) for full credit.
  • 2014-02-21  23:59:59 (that's Fri, 21 Feb 2014, 11:59:59 pm) for 75% credit.

Compiler for Assignments, and for I/O: Study the pages:
Overview: For this recitation you are to do the following:

  • A. Write an R-D parser for a subset of Tiny.
  • B. Add Code to make the program into a compiler.
  • C. Compile 4 Tiny programs to MIPS and run the MIPS with SPIM.
A. Write an R-D Parser for a subset of Tiny:
    Write a program in Java or C that will parse the following grammar, which is a subset of the full language we want to compile:

    Subset Tiny® Grammar
    M  −−>  S { S } '$'
S  −−>  A  |  P  |  G
A  −−>  lower-case '=' E ';'
P  −−>  '<'  E  ';'    |  '<'  ('B' | 'N' | 'T') ';'
G  −−>  '>'  lower-case ';'
E  −−>  T {('+' | '-') T}
T  −−>  F {('*' | '/') F}
F  −−>  '(' E ')'  |  lower-case  |  digit

    This grammar adds just four statements to the grammar for arithmetic expressions that we've been working on: an assignment statement, two kinds of output statements, and an input statement. It also leaves off the hat operator ^, along with the grammar rule for the hat. (This rule uses a non-terminal U in some places and a non-terminal S in others. S is used above for a "statement".) The next table gives an list of these 4 constructs, with the grammar rules and with examples.

    Features Implemented by this Recitation
    Name of Feature Grammar Rule Tiny Examples
    Assignment Statement
    (Insert value into a variable)    		 
    A −−> lower-case '=' E ';'
    		 
    n = n + 1; a = 2*b/c-4;
    Output Expression
    (Output value of an expression)    		 
    P −−> '<' E ';'
    		 
    < n; < (a+b)/2;
    Output Blank, Newline, or Tab
    (B for ' ', N for '\n', T for '\t')    		 
    P −−> '<' ('B' | 'N' | 'T') ';'
    		 
     < B; < N; < T;
    Input Value (Insert value
    from input into a variable)    		 
    G −−> '>' lower-case ';'
    		 
     > n; > a; > p;

    You should test your parser with some of the Tiny programs below.

B. Add Code to Make the program into a compiler:
    How is Memory Mapped: We need to be clear about the use of memory at run time. Recall the .data part of the MIPS code we will use:

    MIPS Memory Allocation
            .data
        .align  3
M:      .double 0.,1.,2.,3.,4.,5.,6.
        .double 7.,8.,9. # constants
        .space  208  # variables a to z
        .space  1000 # 125 temporaries
Blank:  .asciiz " "
NewL:   .asciiz "\n"
Tab:    .asciiz "\t"

    We use M[i] to stand for i*8 bytes past the start of M. Then the locations of digits, variables and temporaries are given in the table: Memory Allocation Table. The names "Blank", "NewL", and "Tab" above are my own arbitrary choice.

    Returning Addresses: Start with your Tiny Parser from Part A above. Each function related to expressions will be returning an address where the value of the corresponding part of the program can be found at run time. Thus functions E, T, and F will each return such an address.

    In my own code I return the proper index of the M "array", and then multiply by 8 before using it, but you could instead return the actual address.

    For example, in your code, whenever you have a call to E, this call should return the address where the value of that expression will be at run time. It doesn't matter whether that call to E processes a digit, an identifier, or an arbitrarily complex expression.

    Consider what the function F should return in your code.

    • If F handles a digit, say stored in a variable ch, then F should return (ch-'0') (or this times 8).
    • If F handles a lower-case letter, stored in ch, then F should return (ch-'a'+10) (or this times 8).
    • If F handles an expression (in parens) by calling E, the F should return whatever E returns (will already be multiplied by 8, if that is the way you are handling things).

    How To Get Started. I would start with the parser from Part A above. Then initially I would make only a few changes:

    1. Change F so that it returns the proper integer for a lower-case letter and the proper one for a digit.

    2. Change T and E so that they pass the value coming to them from below on up by returning it.

    3. Add code to A so that it completely handles an assignment. A first decides which address belongs to the variable on the left side. Save this number inside A. Then get the number returned from a call to E. Multiply this by 8 to get byte offset of the expression from the start of M. (Or you may be working with addresses that are already multiplied by 8.) Finally generate (print) two MIPS instructions, the first to load the number at the locations returned by E into a register, and second to store this number into the location given by the identifier at the right side of the assignment. So start with the input: f = 7;$, which should be a legal input to your parser. With the changes above, your program should output the two MIPS instructions at the far left. Then with the same program, try the second input.

      Sample Input a:
      Input: f = 7; $
Should produce output:
# M[15] = M[7]
        l.d  $f2,  56($s1)
        s.d  $f2, 120($s1)
      		  
      Sample Input b:
      Input: f = 7; g = f; $
Should produce output:
# M[15] = M[7]
        l.d  $f2,  56($s1)
        s.d  $f2, 120($s1)
# M[16] = M[15]
        l.d  $f2, 120($s1)
        s.d  $f2, 128($s1)

    1. Start on the case of handling an arithmetic operator in an expression. This is by far the most difficult part, yet in the end it doesn't take much coding. Do just plus(+) first, and focus on the following example. (Once you have + done, the other three operators are essentially the same.)

      Sample Input c:
      Input: g = f + 8 ; $
Should produce output:
# M[36] = M[15] + M[8]
        l.d    $f2, 120($s1)
        l.d    $f4,  64($s1)
        add.d  $f6, $f2, $f4
        s.d    $f6, 288($s1)
# M[16] = M[36]
        l.d    $f2, 288($s1)
        s.d    $f2, 128($s1)

      You must add to the function E so that when there is an addition, it will produce two loads, add, and a store instruction.

      If there is a +, then inside E, there will be two calls to T, each returning an address taking care of whatever in the tree is below that T. These two addresses are used for the two loads. Then you need to generate a new temporary memory location, and that will be the address in the store instruction. Finally, if there are only two operands in that call to E, the address of the temporary is what E will return.

    More about handling an addition: An addition was discussed and illustrated in Step 4 directly above. Let's go into it in more detail. Simplify the parser code so that it will just handle a single addition, without worrying about several of them. This is the function on the left below. The code beside on the right shows E returning an int to hold an address, the offset from $s1.
    Function E for parser
    void E(void) {

   T();
   if (next == '+') {
      scan();
      T();
   }
}
    		  
    Function E for compiler
    int E(void) {
   int res, arg1, arg2;
   arg1 = T();
   if (next == '+') {
      scan();
      arg2 = T();
   }
   res = // temp address for sum
   return res;
}

    After E gets the two addresses from the two calls to T, it can output an add instruction. First the two operands from the two T's must be loaded. Then the add using registers, and finally a store instruction to stick the result into a new temporary memory location. The diagram below shows this. (Diagram in PDF.)

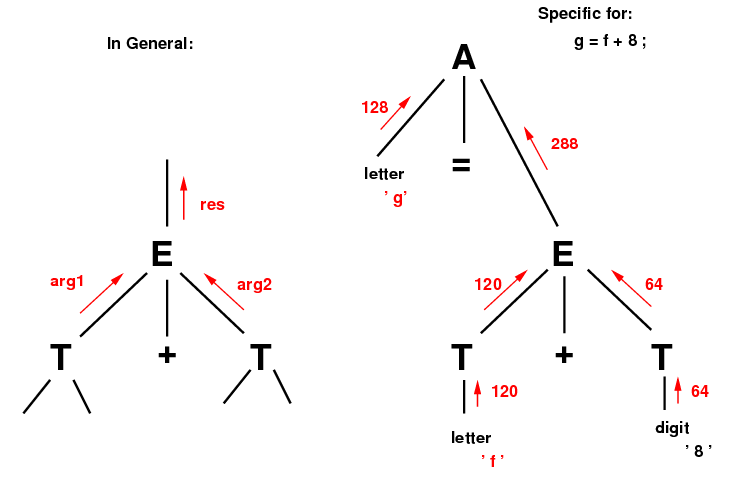
    Very important: In problem 3 of Recitation 3, you translated something like f = g + 5; into 4 MIPS instructions. This was possible because you were looking at the entire statement at once. Your compiler will need 6 statements (as shown above) to translate this. The function E only handles expressions and addition/subtraction. It is completely separate from the function A that handles assignments. E doesn't know where its results are headed, and similarly, A doesn't know where the expression to the right of the assignment operator came from, or anything about this expression. As far as A knows, it could be a single variable, a single constant, or a very complex expression.

C. Compile 4 Tiny programs to MIPS and run the MIPS with SPIM.

    Sample Programs: (In the end, the three inputs above, a, b, and c, are for your own debugging.) Here are sample programs that you should compile from Tiny to MIPS assembly code. You then should execute the MIPS code. For these you need to implement the two types of output In order to successfully execute these using spim, you must add the stuff at the beginning and end of the complete sample programs. Of course all four programs work with doubles, but the doubles in Sample Input 1 are all exact integers.

    Sample
    Input 0:
    a = 8 * 2;
b = 7 * a;
c = b + 1;
d = a / c;
e = 3 + d;
< e;
< N;
$
    		  
    Sample Input 1:
    f = 3*7;  
g = f + (9 + 4);
h = f + g;
< h; < B;
a = f*f + g*g; 
b = g*h + f*g;
c = g*g + h*h;
< c; < B;
f = a*a + b*b;
g = b*c + a*b;
h = c*c + b*b;
< h; < N;
a = f*f + g*g; 
b = g*h + f*g;
c = g*g + h*h;
< c; < N;  $
    Output:
    55 4181 24157817
806515533049393

    Fibonacci Nums:
F10 F19 F37 F73
    		  
    Sample Input 2:
    < 3+1/(7+1/(5*3+1/(1+
1/((4*(9*8+1))+1/(1+
1/(1+1/(1+1/(2+1/(1+
1/(3+1/(1+1/(2*7+1/(2+
1) ))))))))))));$
    		  
    Sample Input 3:
    p = 3 + (1/7);
> r;
v = (4/3)*p*r*r*r;
< p; < N;
< r; < N;
< v; < N;
$
    Run of Program:
    % spim r3.s
3.5
3.14285714285714279
3.5
179.666666666666657

    What you should submit:
    • Give the complete Java or C source code for your compiler program.
    • For each of the four sample program in turn, include:
      • The original Tiny program.
      • The complete MIPS code that results from compiling that Tiny program, for Sample Inputs 0 and 3 only. (My MIPS code for Sample Inputs 1 and 2 are 240 and 180 lines long respectively.)
      • The output resulting from running that particular MIPS program using spim.

Revision date: 2014-01-29. (Use ISO 8601, an International Standard.)