Answers are in red (points in parens).

1. (15)Consider the formal Grammar in the comment at the start of the attached program.
   1. (3)Is this grammar ambiguous? (Yes or No)
   2. (3)What is the associativity of the operator ^? Right-to-left.
      
   3. (3)If we wanted to reverse its associativity, how would we change the grammar? Changing
           S ---> F '^' S | F
      to
           S ---> S '^' F | F
      would make the operator associate Left-to-Right, but now the grammar is no longer appropriate for recursive descent parsing. The correct answer is:

      S ---> F {'^' F}
      

   4. (6)Construct the parse tree for the sentence: 1 * ( 2 + 3^4 ) $ This is a standard parse tree that most students got correct.

   ---

2. (15)This question has to do with finite state machines (FSM).
   1. (3)In class we talked about a FSM being equivalent to a language construct that you have seen elsewhere. What is this construct? I intended for you to answer regular expression, since that is the equivalent "language construct that you have seen elsewhere". However, another correct answer is regular grammar, that is, a formal grammar with all rules of the form:

      A ---> a        (A any non-terminal, a any terminal)
      A ---> a B      (A any non-terminal, a any terminal, B any non-terminal)
      

   2. (4)What is the definition of a language, when the terminal symbols (called the alphabet) consists of the three letters a, b, and c? A language L' over this alphabet is some collection of (finite) strings made up of the three symbols. Thus a language is a subset of the collection L of all finite strings made up of these three symbols. This last set has infinitely many strings in it. Ordered by length and then alphabetically, L would be: L = {e, a, b, c, aa, ab, ac, ba, bb, bc, ca, cb, cc, aaa, aab, ...}. The symbol e stands for the empty string. A language L' is any subset of L, either finite or infinite.

   3. (4)Convert the following FSM to the notation of the other language construct.

      

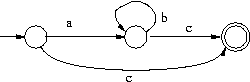
      As a regular expression, the description would be:
           ab*c|c
      or fully parenthesized:
           (((a(b*))c)|c)

      As a regular grammar, the description would be:
           A ---> a B
           A ---> c
           B ---> b B
           B ---> c
      where A is the start symbol.

   4. (4)In both cases these methods are describing or recognizing a language. Describe this language in ordinary English. The language consists of either a single c, or a single a followed by any number (including 0) b's followed by a single c.
      In symbols: L' = {c} union {abⁿc: n >= 0}. Clearly L' is a infinite subset of L from item 2.b above.

   ---

3. (25)Consider the following code. It is my parse function for one of the grammar rules in the Tiny® language. (Your code ought to have been similar. The name of this function has been replaced by a letter X.)

   
      private void X() {
         // 1: start of code to parse the statement
         Declare variable, say "res" and "label"
         (Items given under #2 below could be here instead)
         if (next == '{') {
            scan();
            // 2: start of code to parse next portion
            Output a label, say "Whilestart:"
            res = E();
         }
         else error();
         // 3: start of code to parse next portion
         Output a "lw  $t1" instr., offset 4 times res from base
         Output a "beq $t1, $0" instr., to some label, say "WhileEnd"
         if (next == '?') {
            scan();
            while (next != '}') {
               S();
               // 4: location for code inside loop
               Nothing here (except MIPS code produced by S())
         }
         else error();
         if (next == '}') scan();
         else error();
         // 5: end of code for statement
         Output a "j WhileStart" instr. to match label in #2 above
         Output a label, say "WhileEnd" to match label in #3 above
      }
   

   1. (4)Which language construct it this code for? The "while" loop.
      NOTE: This code could also belong to an "if-then" with no "else" construct. I didn't consider this possibility, because you should not have have had such a function, but only a single "if-the-else" function. However, I gave most of the credit if you treated it this way. The main differences would be not to have a starting label and not to have a jump from just before the end back to this starting label.

   2. (4)Give the grammar rule for this construct. W ---> '{' E '?' { S } '}'

   3. (13)There are numbered locations labeled 1, 2, 3, 4, and 5 in comments. Following each of these locations there may be none, or one, or more than one parts of MIPS code (including possibly labels) that need to be output at this point. Give the MIPS code as well as you can. Show what is done with the value returned by the call to the function E. See above.

   4. (4)There is an extra integer counter value that is used inside this function. What is this counter value for?All labels have to be unique to this particular while statement. One solution is to create a new counter value, store in the variable "label" above, and add this counter value to the end of each label. (There are other ways to accomplish unique labels.)

   ---

4. (20)This is a question about run-time storage management, specifically, support for function call/return.
   1. (3)What kind of object is used to support function call/return? A stack

   2. (3)Does this support recursive functions? (Yes or No).

   3. (5)What kind of information is usually placed in this object during a function call? What form does the information have? At run time, whenever there is a function call, code created by the compiler will push a special block of storage onto the stack called an activation record for the function. This block will usually contain the return address, the return value, pointers to various useful locations, including to the previous activation record on the stack, and storage for parameters and local variables.

   4. (5)Given a function that looks like the following (C/C++ notation):

      
      int F(int x, char y) {
         int a[4] = {1, 2, 3, 4};
         return a[2];
      }
      

      what additional information will be placed in the object? In the case above, there must be room for the two parameters and for the array. This function has a return value that also must be taken care of, probably on the stack.
      Note: The value returned will be copied back, and there will be no problem due to deallocation of the storage for the array.

   5. (4)What happens when the program returns from the function F above? The return address is retrieved from the activation record. The return value must be copied to an appropriate location. The activation record must be popped off the stack, usually just by adjusting the pointer to the top of the stack. Then execution is started up at the point given by the return address.

   ---

5. (25)Consider the attached Java program Paren.java along with sample output. (The separate class GetNext.java just has a method getNextChar() that fetches the next input char.)
   1. (3)What kind of parser is being used in this program? Recursive descent

   2. (3)Briefly say what this program is doing. It is transforming input arithmetic expressions to insert brackets instead of parens, but only when they are used in conjuction with an operator. No parens remain, and no superfluous brackets are used.

   3. (3)Briefly say roughly how it is working. Only when the processor encounters an actual operator with two operands does output a pair of square brackets to surround the operator and its two operands. Inside F, any parentheses, including extra ones, are removed.

   4. (3)Given the input 7 $, what will the output be? 7

   5. (3)Given the input ( ( ( ( 7 + ((4)) ) ) ) ) $, what will the output be? [7+4]

   6. (10)Alter the program so that it outputs Lisp expressions, that is, Lisp S-expressions, which have the form of a parenthesized expression with the operator first, followed by the two operands, separated by at least one blank. The operands have this same structure. Here is what the output should look like. (The column on the right shows the actual Lisp interpreter processing the output.) See ParenLisp.java for an answer.

      % java ParenLisp 1 + 2 * 3 $ (+ 1 (* 2 3)) % java ParenLisp (1 + (2 * 3)) $ (+ 1 (* 2 3)) % java ParenLisp 1*(2+3)$ (* 1 (+ 2 3))

      % lisp > (+ 1 (* 2 3)) 7 > (* 1 (+ 2 3)) 5 > (quit) %