(Click or use local copy.)

CS 3723/3721  Programming Languages  Spring 2005  Recitation 12  Postscript Programs     Week 12: Apr 11-15  Due (on time): 2005-04-18  23:59:59  Due (late):        2005-04-22  23:59:59

Recitation 12 must be submitted following directions at: submissions with deadlines 2005-04-18  23:59:59 (that's Monday, 18 April 2005, 11:59:59 pm) for full credit. 2005-04-22  23:59:59 (that's Friday, 22 April 2005, 11:59:59 pm) for 75% credit.

Part A: Three versions of a Postscript Knot Program
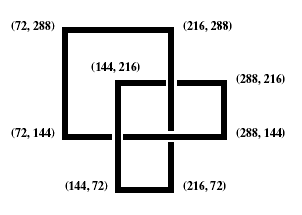
x: 4, vertices labeled	x: 8	x: 12

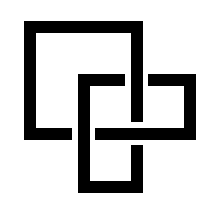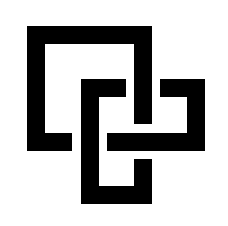You should make x a variable inside the program. You should draw the three line segments that make up the "knot" with linewidth 2*x, and allow a "gap" at either end of each line segment of width x. (The end of each line segment is then a distance of 2*x from the center of the other line segments.) The numbers in the left-hand picture give the coordinates of each corner of the paths used. Notice that these are just whole "inches". You can then get the three pictures above by taking x equal to the value above each picture. (Of course without the numbers in the left-hand picture.) What will the picture look like when x has value 24?

Part B: Return Address for a mailing

For full credit, include the following features:

• the two fields shown must be exactly 0.5 inch (36 points) from the top of an 8.5-by-11 inch sheet of paper,
• margins must be exactly 0.5 inch (36 points).
• The font on the left should be given by Times-Bold findfont 14 scalefont setfont
• The font on the right should be the same, except 12 point
• all linewidths should be given by 2 setlinewidth.
• The length of the lines at the left should be the same as (The University of Texas at San Antonio) stringwidth pop, that is, by the length of this string.
• lines on the left should be 15 points apart vertically.
• lines on the right should be 12 points apart vertically.
• The box on the right should be 132 points wide.
• Each line of the box on the right should be exactly centered in the middle of the box.

The image above is an actual image, 8.5 inches wide, taken from a program that met the requirements above. If you have trouble meeting the above requirements, just fake it as well as you can, and try to make your output look as close to the above as possible.

• n: the number of circles
• r: the radius of each circle
• s: the radius of the circle giving the centers of the circles.

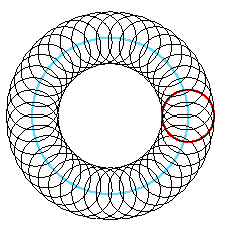
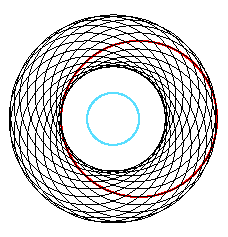
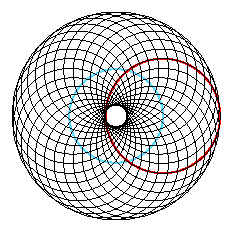
The pictures below give a little more information: In the last 4 pictures the first circle is drawn wider and in red. The circle of the centers of circles is drawn in "CornflowerBlue".

Part C: Circles
n:10, r:100, s:100	n: 20, r:100, s:100	n: 40, r:100, s:100
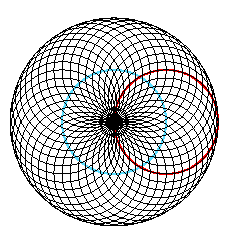n:40, r:50, s:150	n: 20, r:150, s:50	n: 30, r:110, s:90

Implementation: There are several simple ways to program this in Postscript. You should center everything at the origin, translate to the center of the page, and draw everything.

You can let an angle th take on the necessary successive values. Then the center of each circle of radius r will be at the point (s*cos(th), s*sin(th), and you can draw each circle.

Alternatively, you can draw one circle and keep rotating by the successive angle: 360/n.

Then during or before the next class meeting: Wednesday, 20 April 2005 submit actual computer printouts (in person or under my door) containing:

1. Postscript source of the three programs.
2. Pictures of runs for the following cases:
   • Knot: one of the three runs above, along with a run using 24 for n.
   • Return address: Just the one run above.
   • One run from the top three examples, and one run from the bottom three.