 |
CS 3723 Programming Languages |
Machines vs Grammars | |
|
Machines (recognize a language) versus Grammars (generate a language): |
Languages: Start with a finite set of symbols called an alphabet, such as {0, 1}, or {a, b, c, d}, or the set of all Ascii characters. A finite string of these symbols is called a sentence. A language is a set of sentences. Thus a language is just some set of strings of symbols. For example, the set E of all strings of 0s and 1s with an even number of 1s is a language. (E = even parity bit-strings.) Notice that everything is finite except for the language, where in the interesting cases there are infinitely many sentences, as with the example above. We want to give finite descriptions of languages, including infinite languages. Consider another example: the set L of all strings of as and bs that end with "abb". The previous (English) sentence is an informal finite description. It would (of course) be impossible to list the elements of this language, but we could start: L = {abb, aabb, babb, aaabb, ababb, baabb, bbabb, aaaabb, aababb, ...}.
Finite State Machines (FSM): These are also called Finite Automata (FA) (singular: "automaton"). One specific type of FA is called a Non-Deterministic Finite Automaton (NFA). Here is a NFA that recognizes the language L above:
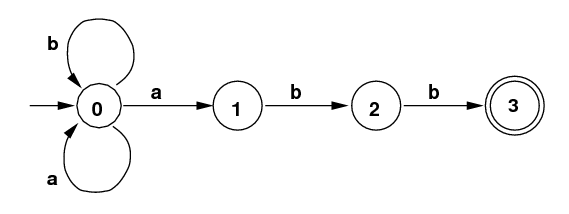
NFA for Language L
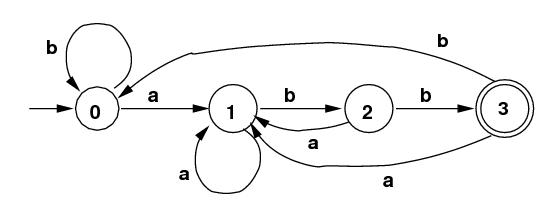
DFA for Language L
Simulating Finite State Machines: We show first DFAs and then NFAs. Simulating a DFA: In a language with labels and gotos, this is easy. Each state becomes a labeled location in a simulation program, and each arrow becomes a goto between the two labeled locations that correspond to the two states. You start at the location corresponding to the start state. You accept if you are in an accepting state (or terminal state) at the end of the string being processed. All this is illustrated with programs to recognize C-style comments: Comments. The above link also shows the use of a while-switch in case gotos are not available or not allowed (say, by an instructor in a course). Simulating an NFA: As you process each input character, your simulating program should keep track of the set of all possible states that you might be in. You start out with the singleton set {start state}. At the end of the input string, if your set of states includes a terminal state, then you accept. Otherwise you reject. (An exercise in Recitation 2 will ask you to carry this process out by hand for a specific string from the language L above.) This same process is essentially the "subset algorithm" that lets one take an NFA and construct a DFA that accepts the same language as the NFA.
Regular Expressions (RE): We will work more with regular expressions later in this course. A regular expression is another way of recognizing or specifying a language. Regular expressions are exactly equivalent to finite state machines. Here is a regular expression that specifies the same language L discussed above:
| Reg Expr |
|---|
| (a|b)*abb |
Formal Grammars: Finally, here is a formal grammar (or context-free grammar or just grammar) that generates exactly the strings of the language L above:
| Grammar Rules |
|---|
|
S ----> a S S ----> b S S ----> a b b |
| Replacement Sequence | ||||||||
|---|---|---|---|---|---|---|---|---|
|
| Replacement Sequence | |
|---|---|
|
Parse Trees: Corresponding to a replacement sequence, we always have a unique parse tree, with the start symbol as the root, and what is replaced at each stage the children:
| Parse Tree | |
|---|---|
S
/ \
b S
/ \
a S
/ \
b S
/|\
a b b |
S
/ \
/ S
/ / \
/ / S
/ / / \
/ / / S
/ / / /|\
b a b a b b
|
Revision date: 2013-09-10. (Please use ISO 8601, the International Standard.)