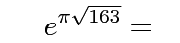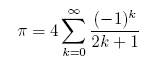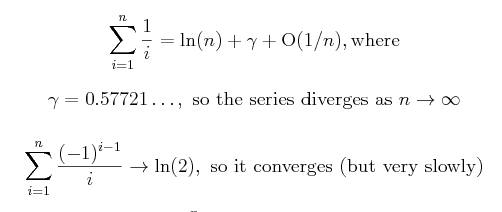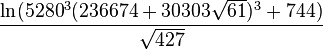| |
The Power of Lisp:
As mentioned above, Common Lisp, and this particular implementation
(clisp), are extremely powerful. Lisp includes almost
any feature you can imagine in a programming language:
arrays. vectors, strings, macros, packages, hash tables,
structures, and even classes that fully support O-O programming
with multiple inheritance.
In addition to the normal data types, this Lisp has:
- Arbitrarily large integers. These are often provided in
the scripting languages, such as perl, ruby, and python.
- Arbitrary precision floats, that is, floats with
arbitrarily many digits of precision (well, bits of course).
The floating point features include all the usual transcendental
functions, also implemented at arbitrary precision. Besides clisp,
there are only a few packages like this available: mainly Mathematica (very
expensive), and Maxima (formerly macsyma, not readily available
or in wide use).
We will show some of this in the computations below:
| High-precision Computations |
|---|
> (factorial 50) ; arbitrarily large ints
30414093201713378043612608166064768844377641568960512000000000000
; the following "magic" command can be copied as it is
> (SETF (EXT:LONG-FLOAT-DIGITS) 200) ; very large floats
200
> (exp (* pi (sqrt 163L0))) ; famous expression
2.6253741264076874399999999999925007259719818568887935385633733699091L17
; rewritten and truncated, this is:
; 262537412640768743.999999999999250072597198
> (defun gr (n) ; Gregory's series for pi/4, recursive
(cond ((= n 0) 1) ; 0 to n inclusive
(t (+ (/ (+ (* (rem n 2) -2) 1)
(+ (* n 2L0) 1L0) )
(gr (- n 1)))) ))
GR
> (* (gr 999) 4L0)
3.1405926538397929259635965028693959704513893307797244893674577835432L0
> (* (gr 10000) 4L0)
*** - Program stack overflow. RESET
> (defun g (n) ; Gregory's series for pi/4, iterative
(setq sum 0)
(dotimes (i n sum) ; i from 0 to n, not including n, sum returned
(setq sum (+ sum (/ (+ (* (rem (+ i 1) 2) 2) -1)
(+ (* i 2L0) 1L0)))) ))
G
> (* (g 1000) 4L0)
3.1405926538397929259635965028693959704513893307797244893674577835432L0
> (* (g 1000000) 4L0) ; 10 seconds elapsed, 5 seconds compiled
3.1415916535897932387126433832791903841971703525001058155647883423586L0
> (* (g 10000000) 4L0) ; 130 seconds elapsed, 60 seconds compiled
3.141592553589793238462893383279502881072169399375201133474944587123L0
> pi
3.14159265358979323846264338327950288419716939937510582097494459230787L0
> (quit)
Bye.
|
The first example above shows 50! calculated,
all 65 digits.
The second example evaluates a famous expression that is
extremely close to an integer:
The third example considers the following series, known
as Gregory's series
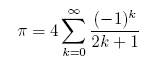This series is similar to the harmonic series that you studied
in calculus, along with the alternating harmonic series:
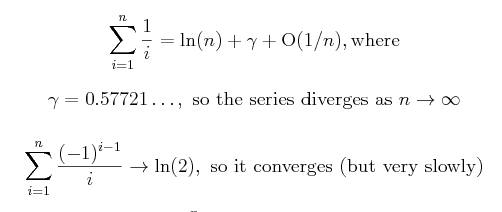Gregory's series also converges very slowly. In fact,
for each additional digit of accuracy in the computation of
π, you need to sum ten times as many terms.
The computations above use a Lisp function g that computes the
sum of n terms of the series for n = 103, 106,
107. These calculations were carried out with roughly
90-digit accuracy (with more for the last one).
The digits that are equal to the digits of
π are given in
blue,
while incorrect digits are given
in red.
(Single isolated digits might agree with probability 0.1, and
most of these have been left red.)
You can see that the value of the sum of 10 ^ i terms has an
error in the ith decimal place (off by 1).
But the table shows an
astonishing number of other digits are equal to the corresponding
digit of π, even though the numbers
themselves are very poor approximations to π.
Can you imagine what is happening here? I also performed all these
calculations in Mathematica and got exactly the same answers.
(There results are an artifact of using a power of 10 as the
number of terms. The last line gives the sum of
9876543 terms of the series, and only a few early digits of it
agree with π.)
| Approximations to
π |
|---|
10^1: 3.0418396189 2940221113
10^2: 3.1315929035 5855276430 7414238276
10^3: 3.1405926538 3979292596 3596502869 3959704513
10^4: 3.1414926535 9004323845 9518383374 8153787870 1364274418 0460513479
10^5: 3.1415826535 8979348846 2643352029 5028937284 1939396494 9575908635 9919594
10^6: 3.1415916535 8979323871 2643383279 1903841971 7035250010 5815564788 3423571533 2034804914 3891718868
10^7: 3.1415925535 8979323846 2893383279 5028810721 6939937520 1133474944 5868976601 5628670236 7768659759
10^8: 3.1415926435 8979323846 2643633279 5028841971 3814937510 5820984475 8423078164 0087605274 8628039759 0335233179 75
pi: 3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 82
ran: 3.1415927548 3979539002 4929611291 2755437003 6080736183 6126709814 8691643667 1905184480 0246716560
|
It is rare for a software package to provide transcendental functions
of arbitrary precision floating point numbers. I also performed most of these
calculations in Mathematica and got exactly the same answers.
For the Lisp function g above, I originally wrote a
recursive version (as I expect students to do), but that version
ran out of stack space when trying to add up 10^4 terms.
The non-recursive
version above had no problem with 10^7 terms at roughly
100 digits, which took 2 minutes on my (slow)
PC workstation.
Basics of Lisp:
- Simple syntax: The Lisp interpreter reads a sequence of
S-expressions.
An S-expressions is either:
- an atom (a constant or identifier), or
- a parenthesized list of S-expressions, separated by
blanks when necessary (and NEVER by commas).
Notice the recursive form of this definition,
showing from the start how important recursion is to Lisp.
Lisp S-expressions always return a result, and they also often have
side-effects, such as defining or invoking functions.
- Constants: The simplest form of S-expression is a constant, which has itself
as value. Lisp is not case-sensitive, but our input to the Lisp
interpreter will be in lower-case, and Lisp will change it to upper-case,
except for letters inside double quotes.
| Atoms |
|---|
> 47 ;;; integer constant
47
> "Lisp" ;;; string constant
"Lisp"
> -.34 ;;; float constant
-0.34
> -.34e-2 ;;; float constant
-0.0034
> 3.141592653589 ;;; float constant
3.1415927
> 3.141592653589d0 ;;; double constant
3.141592653589d0
> 666d0 ;;; double constant
666.0d0
> t ;;; this is true in Lisp
T
> nil ;;; this is false
NIL
> () ;;; this is also false
NIL
> (equal () nil) ;;; they are equal!
T
|
- Simple lists: Given a simple list of atoms, Lisp regards the
first item as a function, makes a list out of the remaining
arguments, and then applies this function to that list of
arguments:
| Evaluating Simple Lists |
|---|
> (+ 8 5)
13
> (/ 355 113)
355/113
> (/ 355.0 113.0)
3.141593
> (/ 355d0 113d0) ; "d0" for "double"
3.1415929203539825d0
> (/ 355L0 113L0) ; "L0" for "extended"
3.1415929203539823009L0
> pi
3.1415926535897932385L0
; 3. 1415926535 8979323846 2643383279
|
- Evaluating lists: The previous section didn't tell the whole
story. When Lisp is given a list, it evaluates the list
(using Lisp function eval). Lisp takes the first
(top-level) element of the list. It must be an atom that represents
a function. Then Lisp evaluates each of the other elements of the
list recursively (again using eval). Lisp makes a
list of these evaluated elements, and applies the first function
to these values (using a Lisp function apply).
Remember: In a simple list being evaluated, the first item
must be the function, and arguments come after.
The arguments are always evaluated first recursively.
| Evaluating Complex Lists |
|---|
> (* (+ (* 5 4) (/ -4 2) ) 37);((5*4)+(-4/2)*37=18*37
666
> (* 2 (asin 1)) ; float: asin(1) = pi/2
3.1415927
> (* 2 (asin 1D0)) ; double
3.141592653589793d0
> (* 2 (asin 1L0)) ; long double
3.1415926535897932385L0
> (+ (* 2 2) (* 3 3) (* 5 5) (* 7 7) (* 11 11)
(* 13 13) (* 17 17)) ; last ')' completes S-expr
666 (Sum of squares of first 7 primes = 666)
|
- Mathematical Functions:
| Mathematical Functions |
|---|
+ - * /
1- 1+ gcd
lcm acos asin
atan cos cosh sin tan
abs ceiling exp floor log
max min mod
round sqrt |
Predicates
(t or nil result)
("p" at end means "has that property") |
|---|
| evenp minusp
oddp plusp zerop
= /=
< > <= >=
|
- Giving atoms a value: Some special functions in Lisp
do not evaluate all their arguments. One such is
setq. It does not evaluate its first argument,
which must be an atom, but it does evaluate its second argument.
In addition, it gives a value to the atom which is its first argument:
| Giving Atoms
a Value |
|---|
> (setq x (+ 7 40)) ; x = 47
47
> (+ 14 x) ; x + 14 == 61
61
> x ; x is still 47
47
> y ; y has no value
*** - EVAL: variable Y has no value
The following restarts are available:
USE-VALUE :R1 You may input a value to be used instead of Y.
STORE-VALUE :R2 You may input a new value for Y.
ABORT :R3 Abort main loop
Break 1 > :r3
> (setq x (/ x 2)) ; first x not evaluated, second one is
47/2
> x
47/2
> (setq x (/ x 2.0)) ; now divide 47/2 by 2.0
11.75
> (quit)
Bye.
elk01:~>
|
Two High-Precision Examples:
Here are two additional formulas, approximating π to
30 and to 52 decimals, taken from a
Wikapedia article:
Approximating π to 30 and to 52 decimals
(Input in red, correct
digits in blue) |
|---|
> (SETF (EXT:LONG-FLOAT-DIGITS) 200)
200
> (defun cube(x) (* x x x))
CUBE
> (/ (log (+ (cube 640320L0) 744L0)) (sqrt 163L0))
3.141592653589793238462643383279726619347549880883522422292962877442L0
> pi
3.1415926535897932384626433832795028841971693993751058209749445923078L0
> (/ (log (+ (cube (* 5280L0 (+ 236674L0
(* 30303L0 (sqrt 61L0))))) 744L0)) (sqrt 427L0))
3.1415926535897932384626433832795028841971693993751058600689073618724L0
> pi
3.1415926535897932384626433832795028841971693993751058209749445923078L0
|
( Revision date: 2014-04-11.
Please use ISO 8601,
the International Standard Date and Time Notation.)
|
