CS 3723
 Programming Languages 
   List Workpage 2  
  Conditionals and Functions  

Lisp Conditionals and Functions: Lisp has a traditional if-then-else but we are going to teach (and use) only the original general cond:

  • cond is another special function that evaluates its arguments in a sequential way:

    Conditional: in place of if-then-else
    (cond
   (pred1  result1)
   (pred2  result2)
   ...
   (t      default))

    Here each predi is a predicate. If pred1 is true, the value of the cond is result1, and no more of the cond is evaluated. Otherwise if pred2 is true, the value of the cond is result2, and no more of the cond is evaluated, and so forth. If none of the predicates is true, then the value will be default.

  • defun is special function that does not evaluate its arguments, but produces the side effect of defining a function. Below shows the form of a definition and of a call.

    defun: define a function
    (defun  fname (v1 v2 ... vn) ; definition of function
   ;; body of function (sequence of S-expressions)
   ;; value of last one is value returned
                )

(fname arg1 arg2 ... argn) ; call of function

    Notice that the form of the call is slightly different from the look of the function definition. In the call, there is a single list with the function name at its head (car). In the function definition the function name is separate, before the list of parameters.

  • In the above fname is the name of the function, v1 v2 ... vn are the n formal parameters which must be identifiers, arg1 arg2 ... argn are the n actual parameters which can be any S-expressions, which will all be evaluated before the function is applied using the supplied definition.
Examples and Problems: This page concludes with a sequence of examples and problems for Recitation 9. The first function we gave was the factorial:

(defun factorial (n) ; a function definition
    (cond ((= n 0) 1)
          (t  (* n (factorial (- n 1)))) ))

Or, using 1- to subtract 1 from a single argument:

(defun factorial (n) ; a function definition
    (cond ((= n 0) 1)
          (t  (* n (factorial (1- n)))) ))

Problem 9.4: Mimic the factorial function above to define a function harmonic, where (harmonic n) returns the value 
     1 + (1/2) + (1/3) + . . . + (1/(n-1)) + (1/n).

  1. First use the operator / with integers, so that the answers are rational numbers. [Try out n = 10, 20. As a check, the value of (harmonic 10) should be 7381 / 2520. See the Questions page for the answer to a question about this problem.]

  2. Then rewrite the harmonic function using constants with a decimal point and with "L0" at the end to force Lisp to use long double numbers. [Now as a check the value of (harmonic 10) should start out 2.928968253968.]

Problem 9.5: Write a recursive function fibonacci that will return the nth fibonacci number F[n], where 
     
F[0] = 0, F[1] = 1, and F[n] = F[n-1] + F[n-2].
[For reference, (fibonacci 10) should return 55, (fibonacci 20) returns 6765 after a few seconds, (fibonacci 30) returns 832040 after a few seconds, and (fibonacci 35) may take a minute to return 9227465.

Problems Involving "raise-to-a-power" or "pow": Consider a recursive function to raise a number to a positive integer power:

pow function
(defun pow (a b)
   (cond ((= b 0) 1)
         (t (* (pow a (1- b)) a)) ))

Notice that here a can be any number at all: integer, float, fraction, zero, positive, negative. In the above program, b is assumed to be a non-negative integer. (The program returns 1 for (pow 0 0), while this should be undefined.)

Question: Without using clisp, try to decide what the result would be if b is negative, say the result of (pow 2 -3). Now actually try this in Lisp.

We would like to print debug information at each recursive invocation of the function

pow function
(defun pow (a b)
   (princ '|pow: |)(prin1 a)(princ '| |)(prin1 b)(terpri)
   (cond ((= b 0) 1)
         (t (* (pow a (1- b)) a)) ))

> (pow 11 6)
pow: 11 6
pow: 11 5
pow: 11 4
pow: 11 3
pow: 11 2
pow: 11 1
pow: 11 0
1771561
> (pow 2972 4)
pow: 2972 4
pow: 2972 3
pow: 2972 2
pow: 2972 1
pow: 2972 0
78018073190656
> (pow 0.3L0 6)
pow: 0.3L0 6
pow: 0.3L0 5
pow: 0.3L0 4
pow: 0.3L0 3
pow: 0.3L0 2
pow: 0.3L0 1
pow: 0.3L0 0
7.2900000000000000015L-4
Close to: 0.000729
> (pow 5/7 5)
pow: 5/7 5
pow: 5/7 4
pow: 5/7 3
pow: 5/7 2
pow: 5/7 1
pow: 5/7 0
3125/16807

Problem 9.6: Modify or rewrite a recursive pow function so that a can still be any number, and b can be any integer, positive, negative, or zero. [Hint: Hey, a^(-b) is just (1/a)^b.]

As tests, calculate

  1. (pow 2 -10),
  2. (pow (pow 2 -10) 10), and
  3. (pow (pow 2 -10) -10)

[As a check, the last value starts out as 1.267650600228L30.]

Problem 9.7: Use your pow to calculate integer powers of the golden ratio, which is φ = (1+sqrt(5))/2. Specifically input

    (SETF (EXT:LONG-FLOAT-DIGITS) 200)

to cause clisp to use longer floating numbers, and then first calculate φ and then calculate φ raised to the power 100 and to the power 121. [As a check, your results should be very close to integers. You will have to remove the scientific notation and move the decimal point to see this. This problem shows that we can generate numbers that are not rational (fractions) and are arbitrarily close to an integer.]

Problem 9.8: Rewrite your pow function as a function rtp ("raise to power", just to have another name) that is based on the recursive definition below. Here we are back to assuming that b is a non-negative integer. [For convenience I wrote and used another lisp function sqr that returns the square of its argument.]

[Um, don't panic. Follow the definition carefully using a cond, with the third case (b = 0) first. To check if b is odd, you can use (=  (rem  b  2)  1).]

After debugging this function (or before if you like), add the debug code to show each recursive function call (the code shown above in red for the second version of the pow function).

For testing, try

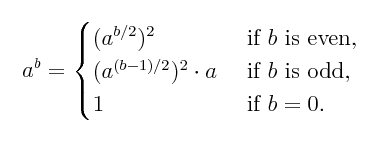
  1. (rtp 7 23)
    [As a check, the answer should be:

    (rtp 7 23)
    > (rtp 7 23)
rtp: 7 23
rtp: 7 11
rtp: 7 5
rtp: 7 2
rtp: 7 1
rtp: 7 0
27368747340080916343

  2. (rtp 2 2143).

  3. How many recursive calls were there in part b above? How many recursive calls would there be with the call (pow 2 2143) where pow is defined as at the beginning of this section? Guess (or figure out) the asymptotic performance of the the rtp algorithm as a function of the second parameter (b)? (Hey, why did you take the algorithms course if not to answer questions like this?)

Revision date: 2013-10-31. (Please use ISO 8601, the International Standard Date and Time Notation.)