CS 3723
 Programming Languages 
   Lisp Workpage 1  
  Simple Calculations  

Lisp Workpage 1: Simple Calculations
  • Mathematical Functions:

    Mathematical Functions
    +   -   *   /   1-   1+   gcd   lcm   acos   asin atan   cos   cosh   sin   tan
    abs   ceiling   exp   floor   log   max   min   mod   round   sqrt
    evenp   minusp   oddp   plusp   zerop   =   /=   <   >   <=   >=

  • Giving atoms a value: Some special functions in Lisp do not evaluate all their arguments. One such is setq. It does not evaluate its first argument, which must be an atom, but it does evaluate its second argument. In addition, it gives a value to the atom which is its first argument:

    Giving Atoms a Value
    > (setq x (+ 7 40))  ; x = 47
47
> (+ 14 x)  ; x + 14 == 61
61
> x  ; x is still 47
47
> y  ; y has no value
*** - EVAL: variable Y has no value
The following restarts are available:
USE-VALUE   :R1 You may input a value to be used instead of Y.
STORE-VALUE :R2 You may input a new value for Y.
ABORT       :R3 Abort main loop
Break 1 > :r3
> (setq x (/ x 2))   ; first x not evaluated, second one is
47/2
> x
47/2
> (setq x (/ x 2.0))  ; now divide 47/2 by 2.0
11.75
> (quit)
Bye.
elk01:~>

    Problem 9.1: Try out numeric computations. Do 
      > (setq a 3)
> (setq b 4)
    and separately calculate each of the three items below: 
      hypotsq = a^2 + b^2
hypot   = sqrt(a^2 + b^2)
vol     = (4/3)*pi*a^3   (answer: vol is 113.097336)
    (You must convert these to Lisp notation, using nested S-expressions, with the function first. Square root is "sqrt". Lisp has no built-in sqr function, though we can easily write one.)

    Problem 9.2: More numeric computations. Do 
      > (setq a 1L0)
> (setq b -1L0)
> (setq c -1L0)
    and separately use setq to assign each of the two items below: 
      r1 = (-b + sqrt(b^2 - 4*a*c))/(2*a)
r2 = (-b - sqrt(b^2 - 4*a*c))/(2*a)
    (Putting an "L0" at the of the constants will force the arithmetic to be done as long doubles.)

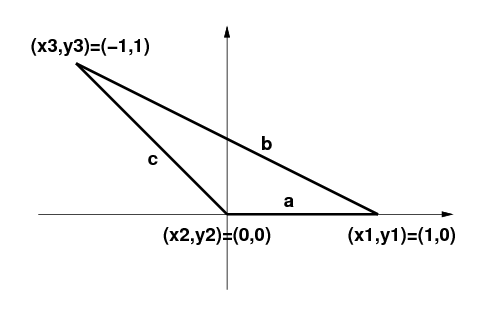
    Problem 9.3: Let (x1,y1) = (1,0), (x2,y2) = (0,0), and (x3,y3) = (-1,1) be the coordinates of the three vertices of a triangle.

      > (setq x1  1)
> (setq y1  0)
> (setq x2  0)
> (setq y2  0)
> (setq x3 -1)
> (setq y3  1)
      		    

    Be careful: Each equation that follows is in ordinary notation, not Lisp notation.
    Convert each of these to Lisp notation, using setq for assignment, and using S-expressions, with the function first.

      a = sqrt((x2 - x1)^2 + (y2 -y1)^2)
    and similarly for b and c, to give lengths of the sides of a triangle. Then set alpha equal to the angle opposite side a as given by the formula: 
      alpha = arccos( (b^2 + c^2 - a^2) / (2*b*c)).
    and similarly for beta and gamma, to give the three angles of the triangle. Finally set 
      sum = alpha + beta + gamma
sumdeg = (180/pi)*sum
    The final answer, sumdeg, should be approximately equal to the sum of the angles of the triangle (which is, of course 180 in degrees).

Revision date: 2013-10-27. (Please use ISO 8601, the International Standard Date and Time Notation.)