| |
|
CS3723, Exam, 17 Oct 2014 |
|
Your Name: |
Hopkins
|
|
G. M.
|
|
|
|
Last |
|
First |
Directions: You may write on the exam or use extra paper or both.
You are not allowed to use anything except the exam sheets.
No crib sheets, no notes, no calculator, no cell phone.
- (20) Grammars: Consider the following grammar
and the sentence to the right of it.
| Grammar |
|---|
E ---> E + T | T
T ---> T * F | F
F ---> ( E ) | id |
| |
| Sentence |
|---|
( id + id ) * id
|
| |
- (2) Is this grammar
ambiguous? (Just Yes or No.)
[It is hard to prove a grammar is not ambiguous.
Ambiguity can easily be proved by displaying a single sentence with
two distinct parse trees.]
- (8) Write out a leftmost
derivation for the sentence.
- (8) Draw a parse tree for the sentence.
- (2) Is there more than one parse tree for the sentence?
(Just Yes or No.) ["No"
because the grammar is not ambiguous.]
|
|
|
1. b.
E ==>
T ===>
T * F ===>
F * F ==>
( E ) * F ==>
( E + T ) * F ==>
( T + T ) * F ==>
( F + T ) * F ==>
( id + T ) * F ==>
( id + F ) * F ==>
( id + id ) * F ==>
( id + id ) * id
| 1. c. E
|
T
+---------------+-----+
T | F
| | |
F | |
+-----------+----------+ | |
| E | | |
| +-----+-----+ | | |
| E | | | | |
| | | | | | |
| T | T | | |
| | | | | | |
| F | F | | |
| | | | | | |
( id + id ) * id
|
- (20) RPN (Reverse Polish Notation):
- (15) Find the value of the following
RPN string using the evaluation method in the homework:
[The blanks are not significant. Each digit is a separate
operand, so there is no integer "56". You must use a stack
and you must show successive stages of the stack as
it evaluates.]
Action Stack (top = right)
push 2 2
push 3 2 3
apply +
pop 3 2
pop 2 -
add:2+3=5
push 5 5
push 4 5 4
apply *
pop 4 5
pop 5 -
mult:5*4=20
push 20 20
push 5 20 5
push 6 20 5 6
apply *
pop 6 20 4
pop 5 20
mult:5*6=30
push 30 20 30
apply +
pop 30 20
pop 20 -
mult:20+30=50
push 50 50
- (5) Give a normal arithmetic expression that represents
this RPN string and has all the same operands in the same order.
(least number of parens): (2 + 3)*4 + 5*6
- (10) Regular Expressions:
Consider the regular expression
/(a|bc*)dd*/=/(ad+)|(bc*d+)/.
In Python this would be written r"(a|bc*)dd*".
Which of the following strings
are described by this RE? (-2 for each mistake, but not below 0)
Any successful string
must end in a d, eliminating (ii) and (v).
Successful string must have a or b, but not both,
eliminating (ii) and (iii). This leaves
(i)=bcd, (iv)=ad, and
(vi)=bd. These are obviously described by the RE.
(i) bcd,
(ii) abc,
(iii) abd,
(iv) ad,
(v) b,
(vi) bd
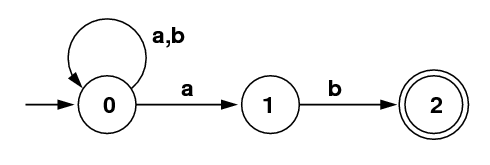
- (20) Subset Algorithm:
Consider the diagram for an NFA at the left below.
|
- (2) How do you know it is an NFA?
Because two arrows labeled with a go from the
state 0 to two different states: 0 and 1. (Even with a DFA, we
may sometimes allow the absence of some arrow, such as no arrow
labeled a from state 1. This would not in itself force
the FA to be an NFA, but would just mean that an a
from state 1 would go to an error state.)
- (2) Give a simple regular expression that describes the
same language that is recognized by this NFA.
/(a|b)*ab/.
- (16) Use the subset algorithm as explained in class to
construct an NFA that recognizes the same language.
[You must first construct a careful DFA table as we have been
doing. Then draw a quick sketch of your DFA.
Be sure to identify the start state and the terminal state(s).]
|
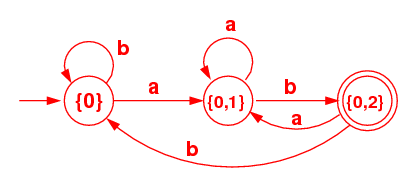
| State | a | b |
|---|
| {0} S | {0,1} | {0} |
| {0,1} | {0,1} | {0,2} |
| {0,2} T | {0,1} | {0} |
|
|
- (20) S-R Parsers: Consider the grammar on the left and
the corresponding parse table for shift-reduce parsing on the right below.
Below those two is the start of the shift-reduce parse of the
sentence:
$ id + id ^ id * id $
. You are to complete this parse, as we did in the
course, step-by-step. In case of an r, give
the grammar rule used. The rule is shown for the first r below.
[A number of students didn't fill in the first
three reduction rules (lines 3-5). It was easy to overlook this, so
I'm not counting it.]
Grammar:
Arithmetic Expressions |
|---|
P ---> E
E ---> E + T | E - T | T
T ---> T * S | T / S | S
S ---> F ^ S | F
F ---> ( E ) | id
|
| Parser: Shift-Reduce Table |
|---|
| id| ^ | */| +-| ( | ) | $ |
---+---+---+---+---+---+---+---+
P | | | | | | |acc|
E | | | | s | | s | r |
T | | | s | r | | r | r |
S | | r | r | r | | r | r |
F | | s | r | r | | r | r |
id | | r | r | r | | r | r |
^ | s | | | | s | | |
*/ | s | | | | s | | |
+- | s | | | | s | | |
( | s | | | | s | | |
) | | r | r | r | | r | r |
$ | s | | | | s | | |
---+---+---+---+---+---+---+---+
|
| |
| Shift-Reduce Actions (Fill in at side and bottom) |
|---|
Stack Curr Rest of Input Action
(top at right) Sym
----------------------------------------------------------------
$ id + id ^ id * id $ s
$ id + id ^ id * id $ r: F --> id
$ F + id ^ id * id $ r: S --> F
$ S + id ^ id * id $ r: T --> S
$ T + id ^ id * id $ r: E --> T
$ E + id ^ id * id $ s
$ E + id ^ id * id $ s
$ E + id ^ id * id $ r: F --> id
$ E + F ^ id * id $ s
$ E + F ^ id * id $ s
$ E + F ^ id * id $ r: F --> id
$ E + F ^ F * id $ r: S --> F
$ E + F ^ S * id $ r: S --> F ^ S
$ E + S * id $ r: T --> S ^ S
$ E + T * id $ s
$ E + T * id $ s
$ E + T * id $ r: F --> id
$ E + T * F $ r: S --> F
$ E + T * S $ r: T --> T * S
$ E + T $ r: E --> E + T
$ E $ r: P --> E
$ P $ acc
|
|
- (20) Subset Algorithm with εmoves:
Consider the NFA with εmoves below. In the diagram, the
symbol '@' stands for ε, the empty string. The arrow from
state 0 to state 1 labeled with a|b|c can be regarded as shorthand for
three arrows, separately labeled with a, b, and c.
For this problem, you are to carry out the first few steps of
constructing a DFA using the subset algorithm.
- (8) Give the start state of the DFA. What is the name of the
algorithm that gives this start state? Say very roughly how
this algorithm works (short answer). The start
state of the DFA is ε-closure({start state of NFA}) =
ε-closure({2}) = state 2 along with all states you can reach from
2 using a sequence of ε transitions.
Intuitively we can reach from 2: 2,0,3; then from 3: 3,14;
then from 14: 14,4,8; or altogether:
ε-closure({2}) = {0,2,3,4,8,14}.
- (6) Give the state that results from processing an a as the
first character. Looking at arrows from elements
of the start state determined in a. above,
we find an arrow labeled a goes
from 0 to 1, from 4 to 5, and from 8 to 9. The states 0, 4, and 8 are
in the start state of the DFA, so the states resulting from
an initial a on input would be
ε-closure({1,5,9}) = {(from 1):1,0,3,14,4,8, (from 5):5,6,
(from 9):9,10} = {0,1,3,4,5,6,8,9,10,14}, so the answer is:
ε-closure({1,5,9}) = {0,1,3,4,5,6,8,9,10,14}.
- (6) Give the state that results from processing a b as the
second character, after the initial a.
This time an arrow labeled b going
from one of the states in part b. above would be
0 going to 1, and 6 going to 7, so the set this time would be
ε-closure({1,7}) = {(from 1):1,0,3,14,4,8,
(from 7):7,15} = {0,1,3,4,7,8,14,15}, so the answer is:
ε-closure({1,7}) = {0,1,3,4,7,8,14,15}.
Note that this is a terminal state.
Thus the string ab is accepted by the NFA and the DFA.
[Some students thought that the answer to this might be the
result of processing an initial character b, which is
the second entry on the first line of the table. This is not correct.
In that case this INCORRECT answer would be:
ε-closure({1}) = {0,1,3,4,8,14}. (INCORRECT answer to
Part c. above.)
I didn't make this my part c., because
it's not very interesting.]

The above is the NFA generated for the RE:
"(a|b|c)*(ab|aac)" .
Here is the result of the subset algorithm on this NFA:
|
NFA for "(a|b|c)*(ab|aac)" |
|---|
| Edges | Graph | Diagram
of DFA |
|---|
states: 16
start: 2
terminal: 15
0 a 1
0 b 1
0 c 1
1 @ 3
1 @ 0
2 @ 0
2 @ 3
3 @ 14
4 a 5
5 @ 6
6 b 7
7 @ 15
8 a 9
9 @ 10
10 a 11
11 @ 12
12 c 13
13 @ 15
14 @ 4
14 @ 8
|
0: [c,1],[b,1],[a,1]
1: [@,0],[@,3]
s 2: [@,3],[@,0]
3: [@,14]
4: [a,5]
5: [@,6]
6: [b,7]
7: [@,15]
8: [a,9]
9: [@,10]
10: [a,11]
11: [@,12]
12: [c,13]
13: [@,15]
14: [@,8],[@,4]
t 15:
|
i | set | a b c
----|------------------|------------
S 0 | 1011100010000010 | 1 2 2
1 | 1101111011100010 | 3 4 2
2 | 1101100010000010 | 1 2 2
3 | 1101111011111010 | 3 4 5
T 4 | 1101100110000011 | 1 2 2
T 5 | 1101100010000111 | 1 2 2
|
Notice that the states have been renumbered from 0 to 5 inclusive.
The states shown in darker red
are answers to the three questions above.
| State | a | b | c |
|---|
| S 0 | {0,2,3,4,8,14} | 1 | {0,1,3,4,5,6,8,9,10,14} | 2 | {0,1,3,4,8,14} | 2 | {0,1,3,4,8,14} |
| 1 | {0,1,3,4,5,6,8,9,10,14} | 3 | {0,1,3,4,5,6,8,9,10,11,12,14} | 4 | {0,1,3,4,7,8,14,15} | 2 | {0,1,3,4,8,14} |
| 2 | {0,1,3,4,8,14} | 1 | {0,1,3,4,5,6,8,9,10,14} | 2 | {0,1,3,4,8,14} | 2 | {0,1,3,4,8,14} |
| 3 | {0,1,3,4,5,6,8,9,10,11,12,14} | 3 | {0,1,3,4,5,6,8,9,10,11,12,14} | 4 | {0,1,3,4,7,8,14,15} | 5 | {0,1,3,4,8,13,14,15} |
| T 4 | {0,1,3,4,7,8,14,15} | 1 | {0,1,3,4,5,6,8,9,10,14} | 2 | {0,1,3,4,8,14} | 2 | {0,1,3,4,8,14} |
| T 5 | {0,1,3,4,8,13,14,15} | 1 | {0,1,3,4,5,6,8,9,10,14} | 2 | {0,1,3,4,8,14} | 2 | {0,1,3,4,8,14} |
Here is a diagram of the final DFA (left)
and of the minimal (I think) DFA (right):
[On the left you can identify states 4 and 5, and
identify states 0 and 2. The renumber to get the DFA
on the left.
Also on left, arrows between states 1 and 2 should be reversed.]
Finally, ...
The original RE:
"(a|b|c)*(ab|aac)" can easily
be written as the following NFA, with no ε-moves:
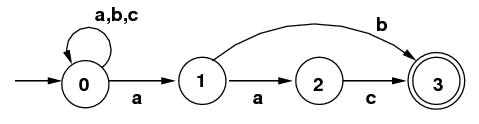 The subset algorithm on this NFA yields the DFA above and
to the right of it. So the question might arise:
Why go to all the trouble above? The answer is that we
want a relatively straightforward way to get an NFA that
represents an arbitrarily complicated RE. We need a systematic
tool, like the one we studied.
The subset algorithm on this NFA yields the DFA above and
to the right of it. So the question might arise:
Why go to all the trouble above? The answer is that we
want a relatively straightforward way to get an NFA that
represents an arbitrarily complicated RE. We need a systematic
tool, like the one we studied.
|



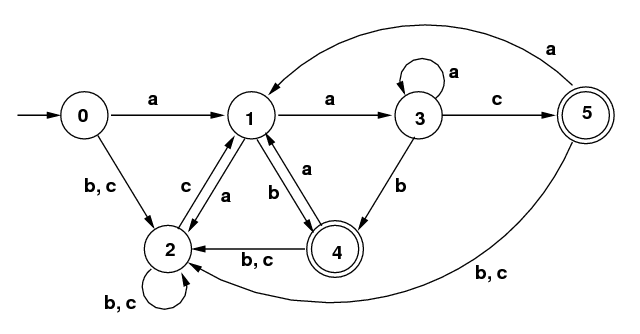
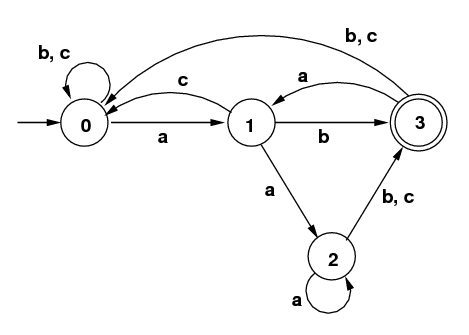
 The subset algorithm on this NFA yields the DFA above and
to the right of it. So the question might arise:
Why go to all the trouble above? The answer is that we
want a relatively straightforward way to get an NFA that
represents an arbitrarily complicated RE. We need a systematic
tool, like the one we studied.
The subset algorithm on this NFA yields the DFA above and
to the right of it. So the question might arise:
Why go to all the trouble above? The answer is that we
want a relatively straightforward way to get an NFA that
represents an arbitrarily complicated RE. We need a systematic
tool, like the one we studied.