| |
- (20) Consider the following grammar
and the sentence to the right of it.
- (2)
Is this grammar
ambiguous? (Just Yes or No.)
- (8)
Write out a leftmost
derivation for the sentence. See below..
- (8)
Draw a parse tree for the sentence.
See below..
- (2)
Is there more than one parse tree for the sentence?
(Just Yes or No.)
E ---> E + T | T
T ---> T * F | F
F ---> ( E ) | id |
| |
( id + id ) * id
| E
|
T
|
+----------+---+
| | |
T | |
| | |
F | |
| | |
+-----+------+ | |
| | | | |
| E | | |
| | | | |
| +--+--+ | | |
| | | | | | |
| E | | | | |
| | | | | | |
| T | T | | |
| | | | | | |
| F | F | | F
| | | | | | |
( id + id ) * id
| E
|
T
/|\
/ | \
T * F
| |
F id
/|\
/ | \
( E )
/|\
/ | \
E + T
| |
T F
| |
F id
|
id
|
|
E ==> T ==> T * F ==> F * F ==> ( E ) * F ==> ( E + T ) * F ==>
( T + T ) * F ==>
( F + T ) * F ==> ( id + T ) * F ==>
( id + F ) * F ==> ( id + id ) * F ==> ( id + id ) * id
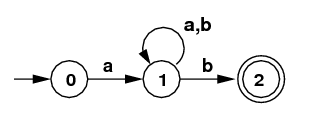
- (20) Consider the NFA below. It comes
from the regular expression /a(a|b)*b/.
| |
Use the subset algorithm from class to construct a DFA
that accepts the same language. For full credit you must show
the subsets. Don't forget to include the empty set.
(Only the pink table below is required,
and not the red diagram.)
|
| Subset Algorithm
(Tables) |
|---|
| NFA,
/a(a|b)*b/ |
|---|
| State | a | b |
|---|
| 0 (start) | 1 | − |
|---|
| 1 | 1 | 1,2 |
|---|
| 2 | − | − |
|---|
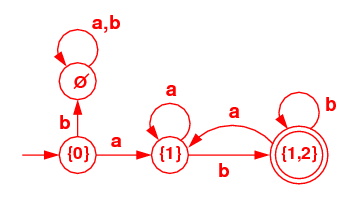
| |
| DFA
|
|---|
| States | a | b |
|---|
| {0} (start) |
{1} | Ø |
|---|
| {1} |
{1} | {1,2} |
|---|
| {1,2} (term) |
{1} | {1,2} |
|---|
| Ø |
Ø | Ø |
|---|
|
- (35) Consider the grammar on the left and
the corresponding parse table for shift-reduce parsing on the right below.
Below those two is the start of the shift-reduce parse of the
sentence:
$ id + id ^ id * id $
. You are to complete this parse, as we did in the
course, step-by-step. In case of an r, give
the grammar rule used. [Be careful: the standard mistake is to
not reduce the longest matching right-hand-side.]
| Grammar: Arithmetic Expressions |
|---|
P ---> E
E ---> E + T | E - T | T
T ---> T * S | T / S | S
S ---> F ^ S | F
F ---> ( E ) | id
|
| |
| Parser: Shift-Reduce Table |
|---|
| id| ^ | */| +-| ( | ) | $ |
---+---+---+---+---+---+---+---+
P | | | | | | |acc|
E | | | | s | | s | r |
T | | | s | r | | r | r |
S | | r | r | r | | r | r |
F | | s | r | r | | r | r |
id | | r | r | r | | r | r |
^ | s | | | | s | | |
*/ | s | | | | s | | |
+- | s | | | | s | | |
( | s | | | | s | | |
) | | r | r | r | | r | r |
$ | s | | | | s | | |
---+---+---+---+---+---+---+---+
|
|
| Shift-Reduce Actions |
|---|
Stack Curr Rest of Input Action
(top at right) Sym
--------------------------------------------------------------------------
$ id + id ^ id * id $ s
$ id + id ^ id * id $ r: F --> id
$ F + id ^ id * id $ r: S --> F
$ S + id ^ id * id $ r: T --> S
$ T + id ^ id * id $ r: E --> T
$ E + id ^ id * id $ s
$ E + id ^ id * id $ s
$ E + id ^ id * id $ r: F --> id
$ E + F ^ id * id $ s
$ E + F ^ id * id $ s
$ E + F ^ id * id $ r: F --> id
$ E + F ^ F * id $ r: S --> F
$ E + F ^ S * id $ r: S --> F ^ S
$ E + S * id $ r: T --> S
$ E + T * id $ s
$ E + T * id $ s
$ E + T * id $ - r: F --> id
$ E + T * F $ - r: S --> F
$ E + T * S $ - r: T --> T * S
$ E + T $ - r: E --> E + T
$ E $ - r: P --> E
$ P $ - acc
|
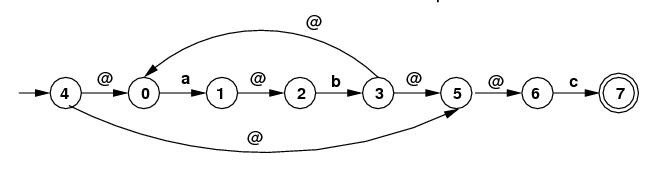
- (20) Consider the NFA with epsilon moves
show below. (Recall the we sometimes use @ in place of
ε.)
- (6)
Give the regular expression that this NFA is derived
from, if one uses the main construction that was presented
in the course. /(ab)*c/
- (4)
Give three distinct strings accepted by this NFA. (No
reason or justification needed.) c, abc, ababc, ...
- (6)
Give the epsilon-closure({4}).
cl({4}) = {0,4,5,6}
(You can construct
it intuitively just by following arrows.)
(4) What is the
significance of this particular set of states?
This is the start state for the DFA
constructed from the above NFA with epsilon-moves
(What is it used for? Short answer.)
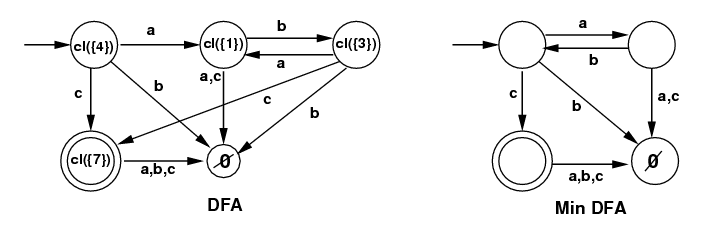
| DFA from NFA,
/(ab)*c/ |
|---|
| States | a | b | c |
|---|
cl({4}) =
{0,4,5,6} (start) |
{cl({1}) =
{1,2} | Ø |
cl({7}) =
{7} |
|---|
cl({1}) =
{1,2} |
Ø | cl({3}) =
{0,3,5,6} | Ø |
|---|
cl({7}) =
{7} (term) |
Ø | Ø | Ø |
|---|
cl({3}) =
{0,3,5,6} |
cl({1}) =
{1,2} | Ø |
cl({7}) =
{7} |
|---|
- (20) In the grammar for the Tiny language
used in class, the rule for an assignment statement is:
A −−> lower-case '=' E ';'
- (16)
With as much detail as you can provide, give your actual code
(in Java or in C) for the function that represents this non-terminal
as part of a recursive-descent parser. (The details of the
language syntax are not as important as knowing what the function
will do.) Just code from the "bare" parser, and just this one
function. However, your code should also check for errors.
- (4)
How does your program decide when to call this function?
(How does the program recognize that it's found an assignment
statement?)
| Parser in Java |
Parser in C |
|---|
private void A() {
if (Character.isLowerCase(next)) {
scan();
}
else error(9);
if (next == '=') scan();
else error(10);
E();
if (next == ';') scan();
else error(11);
} | void A(void) {
if (islower(next)) {
scan();
}
else error(9);
if (next == '=') scan();
else error(10);
E();
if (next == ';') scan();
else error(11);
} |
The assignment statement begins with a lower-case
letter, and it is the only statement that does. The above code
is from my own program. Inside the function S, I check for
a lower-case letter, and without scanning, call A. In A,
I check again for a lower-case letter, though there is no need for this.
Then I finally scan past the letter.
Just for the parser we could scan past the letter just
before calling A. Later, in translating an assignment
to MIPS, the function A will need to know what letter the
assignment started with, and it's more convenient to let
A have access to the letter before scanning. (We could instead
pass the letter to A as a parameter.)
There many other ways to write the function A.
|



