CS 3721
Programming Languages  
Spring 2014
 Recitation 8.   DFAs & NFAs 
Possible Answers in Red 

Finite Automata:
  1. Consider the finite automaton below. (State 9 is an "accepting" state and States 4 and 5 are "error" or "rejecting" states.)


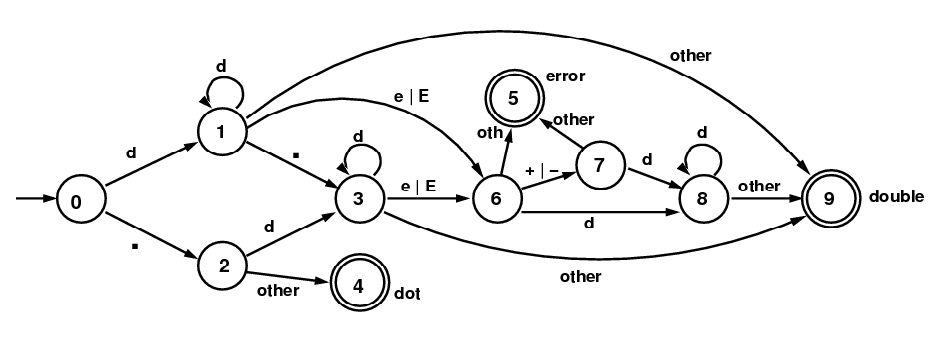
    FSM for doubles, where "d" stands for any digit (the "suffix" is not included)

    1. Is this an NFA or a DFA? (Always give reasons! Because there aren't any two arrows from the same state with the same label.)

    2. Suppose the FA processes the string "13.2$" (where '$' is just a terminator that we will often use.) It will start in State 0 and proceed along from state to state as it processes character after character:

      1 3 . 2 $
      0--->1---> 1--->3---> 3--->9

      Explain why this means it has accepted the string? Duh! Because it ended in the accepting state 9.

    3. Do the same for the string "13E+$"? Explain why the result means that it has not accepted the second string.

      1 3 E + $
      0--->1---> 1--->6---> 3--->5

      Not accepted because it ended in the errror state 5.

    4. Write several strings that are recognized by this FA, and give the sequence of states as above. Include enough examples of strings that are accepted so that every arrow of the diagram is used while accepting one of the example strings. (This does not include arrows pointing to "error" states.) The string below, along with the one in part b, reaches all the non-error states, but it's still missing a few arrows to non-error states.

      . 3 E + 4 $
      0--->2---> 3--->6---> 7--->8--->9

Simulating a DFA:
  1. Write a program in C or in Java, perhaps similar to the one at abb (but it doesn't have to be similar), that will simulate (or model) the actions of the following DFA:


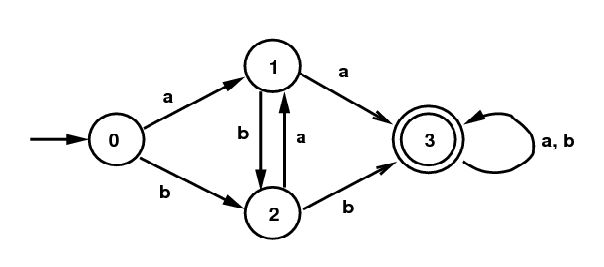
    DFA for   /(a|b)*(aa|bb)(a|b)*/

    Use "babaabab$" and "ababaabbabaaa$" as separate inputs to your program. Your program must print the state number after each input character.

    Note: This problem asks for a program. You must always give the source for any program you are asked to write, and you must always give the results of one or more runs of the program (depending on what input data is given). I do not want a zip of some giant Eclipse directory holding everything, but instead I want a single text file with the source files concatenated together, along with output at the end. Very few changes to the Java code.

Java Program Output
// Prob2.java: recognize (a|b)*abb
import java.io.*;
public class Prob2 {
   private GetChar getChar;
   private char ch;
   private int state = 0;

   public Prob2() {
      getChar = new GetChar();
      state = 0;
   }

   public void process() {
      while (true) {
         ch = getChar.getNextChar();
         if (ch == '$') break; // out of while
         switch (state) {
         case 0: if (ch == 'a') state = 1;
                 else if (ch == 'b') state = 2;
                 break;
         case 1: if (ch == 'a') state = 3;
                 else if (ch == 'b') state = 2;
                 break;
         case 2: if (ch == 'a') state = 1;
                 else if (ch == 'b') state = 3;
                 break;
         case 3: if (ch == 'a') state = 3;
                 else if (ch == 'b') state = 3;
                 break;
         }
         System.out.print("ch: " + ch + ", next state: "
            + state);
         if (state == 3) System.out.print(" Terminal");
         System.out.print("\n");
      }
      if (state == 3) System.out.print("Accept\n");
      else System.out.print("Reject\n");
   }

   public static void main(String[] args) {
      Prob2 prob2 = new Prob2();
      prob2.process();
   }
}

% java Prob2
babaabab$
ch: b, next state: 2
ch: a, next state: 1
ch: b, next state: 2
ch: a, next state: 1
ch: a, next state: 3 Terminal
ch: b, next state: 3 Terminal
ch: a, next state: 3 Terminal
ch: b, next state: 3 Terminal
Accept


% java Prob2
ababaabbabaaa$
ch: a, next state: 1
ch: b, next state: 2
ch: a, next state: 1
ch: b, next state: 2
ch: a, next state: 1
ch: a, next state: 3 Terminal
ch: b, next state: 3 Terminal
ch: b, next state: 3 Terminal
ch: a, next state: 3 Terminal
ch: b, next state: 3 Terminal
ch: a, next state: 3 Terminal
ch: a, next state: 3 Terminal
ch: a, next state: 3 Terminal
Accept

Subset Algorithm:

    You must show your work. You don't need to draw a diagram of the DFA resulting from using the subset algorithm. (You should draw a diagram for your private use in seeing if you seem to have the right answer.) Your answers can look like the items in the link above identified as "Tables" and labeled "DFA". Don't write a table for the input NFA.

  1. Use the subset algorithm to convert the following NFA into a DFA that accepts the same language. (Hint: The DFA also has 4 states.)


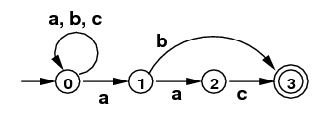
    NFA for   /(a|b|c)*(ab|aac)/
    (Intuitively, any string of "a"s, "b"s, and "c"s,
    ending in "ab" or "aac".)

    Stateabc
    S 0{0} 1{0,1} 0{0} 0{0}
    1{0,1} 2{0,1,2} 3{0,3} 0{0}
    2{0,1,2} 2{0,1,2} 3{0,3} 3{0,3}
    T 3{0,3} 1{0,1} 0{0} 0{0}

    Note that the new subset states above are also renumbered from 0 to 3. Below the answer is given in a form you are more used to.

    Stateabc
    S{0}{0,1}{0}{0}
    {0,1}{0,1,2}{0,3}{0}
    {0,1,2}{0,1,2}{0,3}{0,3}
    T{0,3}{0,1}{0}{0}

  2. Use the subset algorithm to convert the following NFA into a DFA that accepts the same language.


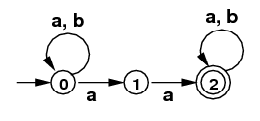
    NFA for   /(a|b)*(aa)(a|b)*/
    (Intuitively, any string of "a"s, and "b"s,
    containing "aa" somewhere.)

    Note: You must use the subset algorithm, and your answer must be what that algorithm generates. (It turns out that the minimal DFA for this language has one fewer state than the result of the algorithm.)

    Stateab
    S 0{0} 1{0,1} 0{0}
    1{0,1} 2{0,1,2} 0{0}
    T 2{0,1,2} 2{0,1,2} 3{0,2}
    T 3{0,2} 2{0,1,2} 3{0,2}

    Again the new subset states are also renumbered from 0 to 3. You can identify the two terminal states: 2 = {0,1,2) and 3 = {0,2}, to get the minimal DFA.

Revision date: 2014-03-24. (Please use ISO 8601, the International Standard.)