CS 3723: Activation Records

	CS 3723 Programming Languages
Activation Records Functions & Recursion

Activation Records in General. If one properly uses a stack at runtime to support function calls, this approach implements recursion "for free", without any additional effort. At run time, each called function is supported by an activation record, which is storage on the stack dedicated to that particular call of that specific function.

The MIPS architecture gives minimal hardware support for recursive functions, so everything must be done "by hand".

The activation record needs to provide storage (at runtime) for at least the following items:

The return address (address from which the function was called). A function might be called from any number of places, including from within itself (recursive call) from any number of places.
The value returned by the function (which might be a pointer).
Locations to hold values of actual parameters fed to the function. (These can be expressions.) After the function is called, these locations function as the formal parameters. They behave like local variables.
Space for (non-static, automatic) local variables used by the function.

The work below uses a running example of a function of two parameters: a "raise-to-a-power" function. This has two parameters and doesn't require any local variables besides registers, so the activation record will hold 4 items, as shown in the illustration below. (The order of these items was an arbitrary choice.) This diagram shows the stack before the function is called. The "stack pointer", denoted by $sp, points to one location beyond the top of the stack, that is, it points to the first available location. Since we are working with doubles, we will only consider 8-byte items on the stack, although the return address takes up only 4 bytes.

[The diagrams show the special MIPS "stack pointer" $sp used to access the MIPS system stack. This is what one would normally use. In order to avoid any possible problems with the official stack pointer, I chose to allocate storage on a user-defined stack pointer, using the register $s2 for it. We have been using $s1 to save the return address of our MIPS function main.]

In the diagram below, the stack pointer "old $sp" might be pointing to the bottom of the stack, with nothing below it. Alternatively, which is below will be the mostly recently called function that is still active (has not yet returned). Assume that the next thing to do is to call a function (in fact a pow or rtp function). The old $sp calculates the two actual parameters, and inserts them into the stack, into locations that will be part of the activation record of the function to be called. These locations are shown in red below.

Stack for Activation Records: Before Function Is Called,
First Insert Parameter Values

                   STACK
                |              |                    |  Next (recursive)
                |--------------|                    |  Activation
                |              |                    |  Record
             ===|==============|===          -------+
   old -24 ---> |  Insert P2   |                    |
                |--------------|                    |  Space for Next
   old -16 ---> |  Insert P1   |                    |  Activation
                |--------------|                    |  Record
   old -8  ---> |              |                    |  (or first one)
                |--------------|                    |  
   old $sp ---> |              |                    |
             ===|==============|===          -------+
   old +8  ---> |  Parameter 2 |                    |
                |--------------|                    |  Previous (current)
   old +16 ---> |  Parameter 1 |                    |  Activation
                |--------------|                    |  Record
   old +24 ---> | Return value |                    |  (if present)
                |--------------|                    |  
   old +32 ---> | Return addr  |                    |
             ===|==============|===         --------+

After the function is called (control is passed to the function), the function first allocated an activation record on the stack, in this example by decrementing the $sp by 32 ($sp = $sp - 32). (This stack is growing toward smaller memory locations.) The function can now "find" the values of actual parameters at known offsets. These locations become the formal parameters for the function. First the function inserts its return address into the activation record (MIPS gives access to this return address). Then the function does its computations, ending with a value to return, which is inserted into the activation record. During its execution, the function may have called other functions, and each of those will push additional activation records onto the stack. By the time this function returns, all other called functions will have returned, so there is nothing above the current activation record. Finally, the called function deletes (deallocates) its activation record by incrementing $sp by 32. The function then returns control to the place from which is was called.

[It's important to realize that there is only one register $sp. "Old" and "new" above refer to different values stored in the register at different times.]

Stack for Activation Records: Function Executes,
Insert RetAdd, Calculate and Insert Return Value

                   STACK
                |              |                    |  Next (recursive)
                |--------------|                    |  Activation
                |              |  <--- new $sp      |  Record
             ===|==============|===          -------+
   old -24 ---> |  Parameter 2 |  <--- new +8       |
                |--------------|                    |  New (current)
   old -16 ---> |  Parameter 1 |  <--- new +16      |  Activation
                |--------------|                    |  Record
   old -8  ---> | Insert RetVal|  <--- new +24      |  
                |--------------|                    |  
   old $sp ---> | Insert RetAdd|  <--- new +32      |
             ===|==============|===          -------+
   old +8  ---> |  Parameter 2 |                    |
                |--------------|                    |  Old (previous)
   old +16 ---> |  Parameter 1 |                    |  Activation
                |--------------|                    |  Record
   old +24 ---> | Return value |                    |  (if present)
                |--------------|                    |  
   old +32 ---> | Return addr  |                    |
             ===|==============|===         --------+

Now, as shown below, the calling function can access the value returned by the function that it called. The calling function will usually have its own activation record (as shown), but it is the main function, it will have no activation record.

Stack for Activation Records: After Function Returns,
Retrieve Return Value

                   STACK
                |              |                    |  Next (recursive)
                |--------------|                    |  Activation
                |              |   <--- new $sp     |  Record
             ===|==============|===          -------+
   old -24 ---> |  Parameter 2 |   <--- new +8      |
                |--------------|                    |  Old deallocated
   old -16 ---> |  Parameter 1 |   <--- new +16     |  Activation
                |--------------|                    |  Record
   old -8  ---> |Retrieve RetV |   <--- new +24     |  
                |--------------|                    |  
   old $sp ---> |  Old RetAdd  |   <--- new +32     |
             ===|==============|===          -------+
   old +8  ---> |  Parameter 2 |                    |
                |--------------|                    |  Current (restored)
   old +16 ---> |  Parameter 1 |                    |  Activation
                |--------------|                    |  Record
   old +24 ---> | Return value |                    |  (if present)
                |--------------|                    |  
   old +32 ---> | Return addr  |                    |
             ===|==============|===         --------+

Our Specific Example: c = a ^ b. We will start with a simple pow function: MIPS code pow0.s below. Then we will rewrite it as a recursive function using activation records as illustrated above. This will be MIPS code powr.s below. Finally, in the next section we'll implement a much more complicated and efficient recursive raise-to-a-power algorithm, where the recursion is not trivial.

I'm thinking in terms of taking input variables a and b, calculating a^b, and leaving the result in a variable c. However, in order to keep things simpler and shorter, I'm not using any memory locations below for variable, but I'm only using registers. How there double registers are used is shown in the first table on the left below.

The MIPS program on the left below shows a very simple loop to calculate a^b, using the register conventions. The MIPS program on the right uses recursion instead of a loop. This program uses a single sequence of recursive calls, so that at the end we can see all the activation records that were used. (None of the storage was overwritten during execution. In more complex programs, the stack of activation records might grow and shrink many times.) The diagram on the left below shows the 11 activation records used to calculate 7^10, at levels 0 (the first one), through 10.

Variables to Registers
# mapping of variables to registers: # $f0 (used for input) # a = $f2 # b = $f4 # c = $f6 # 0 = $f8 # 1 = $f10 # $f12 (used for output) # $f14 (for return value) # 2 = $f16 # $f18 (temporary)

a^b, with simple loop

### pow0.s: calculate c = a^b main: addu $s7, $ra, $zero # addr of M: constants, vars, temps la $s1, M # read a as double li $v0, 7 syscall mov.d $f2, $f0 # read b as double li $v0, 7 syscall mov.d $f4, $f0 ### end reading, start processing l.d $f8, 0($s1) # 0.0 l.d $f10, 8($s1) # 1.0 l.d $f6, 8($s1) # c = 1 WhileStart0: c.eq.d $f4, $f8 # if b==0 bc1t WhileEnd0 mul.d $f6, $f6, $f2 #c=c*a sub.d $f4, $f4, $f10#b=b-1 j WhileStart0 WhileEnd0: ### return to system addu $ra, $s7, $zero jr $ra .data .align 3 M: .double 0.,1. Blank: .asciiz " " NewL: .asciiz "\n"

Level	Activation Records for 7^10
Level	P 2	P 1	Return Value	Ret Addr
10	0	7	1	4194656
9	1	7	7	4194656
8	2	7	49	4194656
7	3	7	343	4194656
6	4	7	2401	4194656
5	5	7	16807	4194656
4	6	7	117649	4194656
3	7	7	823543	4194656
2	8	7	5764801	4194656
1	9	7	40353607	4194656
0	10	7	282475249	4194396

a^b, recursive

### powr.s: act. records and recursion
main:   addu    $s7, $ra, $zero
# addr of S, M: stack, constants
        la      $s2, S
        la      $s1, M
### start of compiled code
# 2 constants
        l.d     $f8,   0($s1)  # 0.0
        l.d     $f10,  8($s1)  # 1.0
# read a as double, store as param1
        li      $v0, 7
        syscall
        s.d     $f0, -16($s2)
# read b as double, store as param2
        li      $v0, 7
        syscall
        s.d     $f0, -24($s2)
# call function
        jal     pow
        l.d     $f14, -8($s2) # ret val
# print return value
        li      $v0, 3
        l.d     $f12, -8($s1)
        syscall
# print NewL as ASCII char
        li      $v0, 4
        la      $a0, NewL
        syscall
# return to system
        addu    $ra, $s7, $zero
        jr      $ra
########## body of pow function #######
pow:
# push activation record
        addi    $s2, $s2, -32
# save return address on stack
        sw      $ra, 32($s2)
# load parameters
        l.d     $f2, 16($s2) # a
        l.d     $f4, 8($s2)  # b
# main part of function
        l.d     $f6, 8($s1)  # c = 1
# check for end to recursion
        c.eq.d  $f4, $f8     # if b==0
        bc1t    RecursEnd
# get ready for recursive call
        sub.d   $f4, $f4, $f10 # b=b-1
# insert 1st and 2nd parameters
        s.d     $f2, -16($s2)  # a
        s.d     $f4, -24($s2)  # b-1
# call function (recursive)
        jal     pow
        l.d     $f14, -8($s2) # ret val
# multiply value returned by a
        mul.d   $f6, $f14, $f2  # c=c*a
RecursEnd:
# insert return value
        s.d     $f6, 24($s2)
# restore return address from stack
        lw      $ra, 32($s2)
# pop activation record
        addi    $s2, $s2, 32
# return
        jr      $ra
######### end of pow function #########
        .data
        .align  3
T:      .space  1000
S:
M:      .double 0.,1.
Blank:  .asciiz " "
NewL:   .asciiz "\n"
Tab:    .asciiz "\t"

Fancy Exponentiation. This example uses a more complex raise-to-a-power algorithm, given by the equations below. Here the recursion is essential, unless one completely rewrites the algorithm. However, again in this case there is only a single tower of recursive calls, so that a dump at the end again shows all the activations records. At the end are two tables showing them for two example runs.

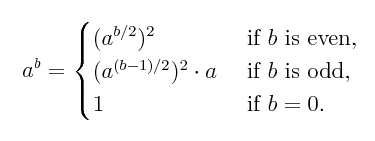
a^b, Fancy Algorithm

### rtp.s: use activation records
main:   addu    $s7, $ra, $zero
# addr of S, M: stack, constants
        la      $s2, S
        la      $s1, M
# 3 constants
        l.d     $f8,   0($s1) # 0.0
        l.d     $f10,  8($s1) # 1.0
        l.d     $f16, 16($s1) # 2.0
# read a as double, store as param1
        li      $v0, 7
        syscall
        s.d     $f0, -16($s2)
# read b as double, store as param2
        li      $v0, 7
        syscall
        s.d     $f0, -24($s2)
# call function
        jal     rtp
# get return value
        l.d     $f14, -8($s2)
# print return value
        li      $v0, 3
        l.d     $f12, -8($s1)
        syscall
# print NewL as ASCII char
        li      $v0, 4
        la      $a0, NewL
        syscall
# return to system
        addu    $ra, $s7, $zero
        jr      $ra
######### body of rtp function ####
rtp:
# push activation record
        addi    $s2, $s2, -32
# save return address on stack
        sw      $ra, 32($s2)
# load parameters
        l.d     $f2, 16($s2) # a
        l.d     $f4, 8($s2)  # b
# start main part of function
        l.d     $f6, 8($s1)  # c=1
# check for end to recursion
        c.eq.d  $f4, $f8 # if b==0
        bc1t    RecursEnd

# next check for even b
        div.d   $f18, $f4, $f16  # t1 = b/2
        trunc.w.d $f18, $f18  # trunc(b)
        cvt.d.w $f18, $f18    # to double
        mul.d   $f18, $f18, $f16 # mult by 2
        sub.d   $f18, $f4, $f18
        c.eq.d  $f18, $f8  # res comp to 0
        bc1f    BisOdd
# here b is non-zero and even
  # get ready for recursive call
        div.d   $f4, $f4, $f16 # b = b / 2
  # insert 1st and 2nd parameters
        s.d     $f2, -16($s2)  # a
        s.d     $f4, -24($s2)  # b/2
  # call function (recursive)
        jal     rtp
        l.d     $f14, -8($s2) # return val
  # square return value, result in c
        mul.d   $f6, $f14, $f14  # c = ret^2
        b       RecursEnd
BisOdd:
# here b is non-zero and odd
  # get ready for recursive call
        sub.d   $f4, $f4, $f10 # b = b - 1
        div.d   $f4, $f4, $f16 # b = b / 2
  # insert 1st and 2nd parameters
        s.d     $f2, -16($s2)  # a
        s.d     $f4, -24($s2)  # b/2
  # call function (recursive)
        jal     rtp
        l.d     $f14, -8($s2) # return val
  # square return value, result in c
        mul.d   $f6, $f14, $f14  # c = ret^2
  # multiply by a
        mul.d   $f6, $f6, $f2
RecursEnd:
# insert return value
        s.d     $f6, 24($s2)
# restore return address from stack
        lw      $ra, 32($s2)
# pop activation record
        addi    $s2, $s2, 32
# return
        jr      $ra
######### end of pow function ###########
        .data
        .align  3
T:      .space  1000
S:
M:      .double 0.,1.,2.
Blank:  .asciiz " "
NewL:   .asciiz "\n"

Level	Activation Records for 2^973
Level	P 2	P 1	Return Value	Ret Addr
10	0	2	1	4194720
9	1	2	2	4194720
8	3	2	8	4194720
7	7	2	128	4194720
6	15	2	32768	4194688
5	30	2	1073741824	4194688
4	60	2	1.15292150e+18	4194720
3	121	2	2.65845599e+36	4194720
2	243	2	1.41347765e+73	4194688
1	486	2	1.99791907e+146	4194720
0	973	2	7.98336123e+292	4194400

L	Activation Records for φ^57				(Return Value)/sqrt(5)
L	P 2	P 1	Return Value	Return Address	(Return Value)/sqrt(5)
6	0	φ	1	4194720	0.4472135954999579≐F(0)=0
5	1	φ	1.6180339887498949	4194720	0.7236067977499789≐F(1)=1
4	3	φ	4.23606797749978981	4194720	1.8944271909999157≐F(3)=2
3	7	φ	29.0344418537486355	4194688	12.984597134749391≐F(7)=13
2	14	φ	842.998813758710526	4194688	377.0005305032323≐F(14)=377
1	28	φ	710646.999998593121	4194720	317811.0000006294≐F(28)= 317811
0	57	φ	817138163596.000732	4194400	365435296162.0003≐F(57)= 365435296162

Revision date: 2013-11-20. (Please use ISO 8601, the International Standard.)