CS 3343/3341
Analysis of Algorithms
  Strassen's Method for  
   Multiplying Matices  

Introduction.

All calculations in this analysis simply count the total number of multiplications, additions, and subtractions. (Thus all three are given equal weight.)

First let T(n) represent the total number of operations (multiplications and additions only in this case) using the ordinary method of matrix multiplication for n-by-n matrices. If n is an exact power of 2 then a divide-and-conquer approach leads to the following recurrence which gives the count:

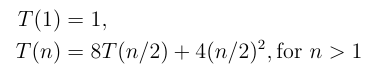
In this case the divide-and-conquer approach leads to exactly the same number of operations as the "normal" method of matrix multiplication. The recurrence above comes from the fact that the normal method, when applied to 2-by-2 matrices, requires 8 multiplications and 4 additions. There is a simple closed form solution for this: T(n) = 2*(n3) - (n2). Separately there are n3 multiplications and n3 - n2 additions. Notice that there are Θ(n3) multiplications and Θ(n3) additions.

Strassen's Method and Its Recurrence.

In 1969, V. Strassen discovered a clever way to multiply 2-by-2 matrices, using 7 multiplications and 18 additions and subtractions. Later, the number of additions and subtractions was reduced to 15, and this latter number is what is used in the calculations below. Some people think that Strassen's discovery had a major impact on the emphasis toward asymototic estimates in the analysis of algorithms, where this means a concern only with results as the problem size tends to infinity. See Strassen's method for details of how he carried out the multiplication.

A normal human being would not think it an improvement to go from 12 operations to 22 operations, but in fact the important part is that Strassen reduced the multiplications from 8 to 7. Asymtotically it doesn't matter how many additions and subtractions there are, because they are Θ(n2). Intuitively, matrix multiplication in the ordinary way is much more complicated than addition, and it is after all a Θ(n3) algorithm.

Assuming that n is a power of 2, a divide-and-conquer approach using Strassen's basic method, in the form using the fewest additions and subtractions, has a recurrence

Solution of Strassen's Recurrence.

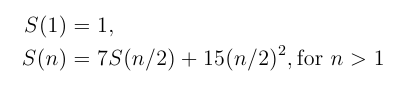
In your text, the recurrence formula for S(n) above is solved in a more general form using the Master Theorem. This is not satisfactory for newcomers, so I'm presenting a solution of the formula from scratch here.

Look at the first few cases of the formula for n a power of 2:

Simplifying and factoring out the highest power of 7, we get formulas like

In general,

The series above inside the square brackets is the initial part of an infinite geometric series that sums to exactly 1/3:

Thus

where k = log2n, and the < inequality is very close to an equality for large n.

Notice that the number of additions, 15, only contributes in the final formulaa to the constant 6. If we used Strassen's original formula, with 18 additions, that number would be a 7, but the final Big-Θ formula would be the same.

Improving the formulas by being practical.

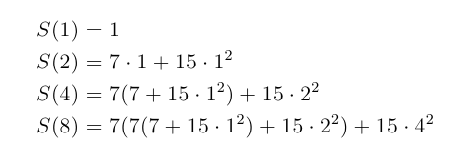
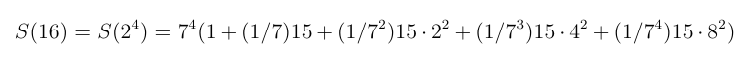
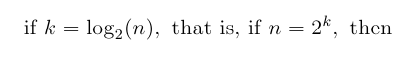
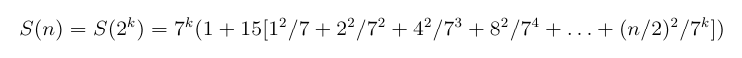
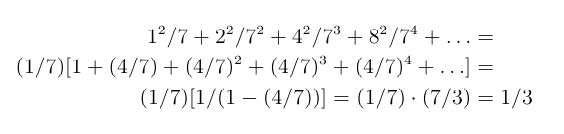
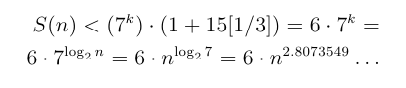
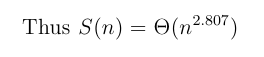
For small n, Strassen's method is worse than the obvious method, so a good algorithm should switch to the obvious method for n below a certain threshold, called lim below. The recurrence for this refinement is

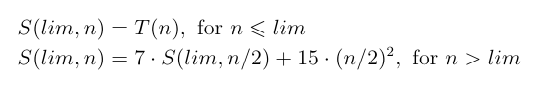
The Table 1 below just gives T(n), S(n) = S(1,n), S(2,n), S(4,n), and S(8,n) for n a power of 2 from 2 to 1024. Notice that S(8,16) < T(16), so we would not want to use S(lim,n) for lim > 8.

The Table 2 below presents the same information for n from 2 up to 240. However, the values of the S(lim,n) are shown as a percent of the basic value T(n). Additionally, the table gives the three ratios of T(n)/(n3), S(n)/(n2.81), and S(8,n)/(n2.81). This shows clearly that

Table 1. Values for T and S with n a power of 2
(Boldface: S is better than T)
    n           T(n)         S(1,n)         S(2,n)         S(4,n)         S(8,n)

    2             12             22             12             12             12
    4            112            214            144            112            112
    8            960           1738           1248           1024            960
   16           7936          13126           9696           8128           7680
   32          64512          95722          71712          60736          57600
   64         520192         685414         517344         440512         418560
  128        4177920        4859338        3682848        3145024        2991360
  256       33488896       34261126       26025696       22260928       21185280
  512      268173312      240810922      183162912      156809536      149280000
 1024     2146435072     1689608614     1286072544     1101598912     1048892160

Table 2. Ratios of different versions of S to T with n a power of 2
                       S(1,n)   S(2,n)   S(4,n)   S(8,n)      T(n)    S(1,n)   S(8,n)
  n          T(n)      ------%  ------%  ------%  ------%    ------   ------   ------
                        T(n)     T(n)     T(n)     T(n)         3       2.81     2.81
                                                               n       n        n

2^ 1    1.200000e+01   183.33   100.00   100.00   100.00     1.5000   3.1429   1.7143
2^ 2    1.120000e+02   191.07   128.57   100.00   100.00     1.7500   4.3673   2.2857
2^ 3    9.600000e+02   181.04   130.00   106.67   100.00     1.8750   5.0671   2.7988
2^ 4    7.936000e+03   165.40   122.18   102.42    96.77     1.9375   5.4669   3.1987
2^ 5    6.451200e+04   148.38   111.16    94.15    89.29     1.9688   5.6954   3.4271
2^ 6    5.201920e+05   131.76    99.45    84.68    80.46     1.9844   5.8259   3.5577
2^ 7    4.177920e+06   116.31    88.15    75.28    71.60     1.9922   5.9005   3.6323
2^ 8    3.348890e+07   102.31    77.71    66.47    63.26     1.9961   5.9432   3.6749
2^ 9    2.681733e+08    89.80    68.30    58.47    55.67     1.9980   5.9675   3.6993
2^10    2.146435e+09    78.72    59.92    51.32    48.87     1.9990   5.9814   3.7132
2^11    1.717567e+10    68.95    52.51    44.99    42.84     1.9995   5.9894   3.7212
2^12    1.374222e+11    60.37    45.98    39.41    37.53     1.9998   5.9939   3.7257
2^13    1.099445e+12    52.84    40.26    34.50    32.86     1.9999   5.9965   3.7283
2^14    8.795825e+12    46.25    35.23    30.20    28.76     1.9999   5.9980   3.7298
2^15    7.036767e+13    40.47    30.83    26.43    25.17     2.0000   5.9989   3.7306
2^16    5.629457e+14    35.42    26.98    23.13    22.03     2.0000   5.9994   3.7311
2^17    4.503582e+15    30.99    23.61    20.24    19.27     2.0000   5.9996   3.7314
2^18    3.602873e+16    27.12    20.66    17.71    16.87     2.0000   5.9998   3.7316
2^19    2.882301e+17    23.73    18.08    15.50    14.76     2.0000   5.9999   3.7317
2^20    2.305842e+18    20.76    15.82    13.56    12.91     2.0000   5.9999   3.7317
2^21    1.844674e+19    18.17    13.84    11.86    11.30     2.0000   6.0000   3.7317
2^22    1.475739e+20    15.90    12.11    10.38     9.89     2.0000   6.0000   3.7318
2^23    1.180592e+21    13.91    10.60     9.08     8.65     2.0000   6.0000   3.7318
2^24    9.444733e+21    12.17     9.27     7.95     7.57     2.0000   6.0000   3.7318
2^25    7.555786e+22    10.65     8.11     6.95     6.62     2.0000   6.0000   3.7318
2^26    6.044629e+23     9.32     7.10     6.09     5.80     2.0000   6.0000   3.7318
2^27    4.835703e+24     8.15     6.21     5.32     5.07     2.0000   6.0000   3.7318
2^28    3.868563e+25     7.13     5.44     4.66     4.44     2.0000   6.0000   3.7318
2^29    3.094850e+26     6.24     4.76     4.08     3.88     2.0000   6.0000   3.7318
2^30    2.475880e+27     5.46     4.16     3.57     3.40     2.0000   6.0000   3.7318
2^31    1.980704e+28     4.78     3.64     3.12     2.97     2.0000   6.0000   3.7318
2^32    1.584563e+29     4.18     3.19     2.73     2.60     2.0000   6.0000   3.7318
2^33    1.267651e+30     3.66     2.79     2.39     2.28     2.0000   6.0000   3.7318
2^34    1.014120e+31     3.20     2.44     2.09     1.99     2.0000   6.0000   3.7318
2^35    8.112964e+31     2.80     2.13     1.83     1.74     2.0000   6.0000   3.7318
2^36    6.490371e+32     2.45     1.87     1.60     1.52     2.0000   6.0000   3.7318
2^37    5.192297e+33     2.14     1.63     1.40     1.33     2.0000   6.0000   3.7318
2^38    4.153837e+34     1.88     1.43     1.23     1.17     2.0000   6.0000   3.7318
2^39    3.323070e+35     1.64     1.25     1.07     1.02     2.0000   6.0000   3.7318
2^40    2.658456e+36     1.44     1.09     0.94     0.89     2.0000   6.0000   3.7318

Program 1. c program to calculate values in previous tables
/* Program to calculate recurrences related to Strassen's
 * method for carrying out matrix multiplication.
 * Written by Neal R. Wagner.
 */
#include <stdio.h>
#include <math.h>
double T(double);
double S(double, double);
main() {
   long i;
   double tpercent; /* T(n) as a percent */
   double log2of7;  /* log base 2 of 7 */
   double N = 2.0;
   double Ncubed, Ntolog2of7; /* N^3 and N^(2.81) */
   for (i = 0; i < 10; i++) {
      printf("%5.0f%15.0f%15.0f%15.0f%15.0f%15.0f\n",
         N, T(N), S(1,N), S(2,N), S(4,N), S(8,N));
      N = N*2.0;
   }
   N = 2;
   log2of7 = log(7)/log(2); /* = 2.807354922... */
   for (i = 0; i < 40; i++) {
      tpercent = T(N)/100.0;
      Ncubed = exp(3.0 * log(N));
      Ntolog2of7 = exp(log2of7 * log(N));
      printf("2^%2ld%16.6e%9.2f%9.2f%9.2f%9.2f%11.4f%9.4f%9.4f\n",
        (i+1), T(N), S(1,N)/tpercent, S(2,N)/tpercent,
         S(4,N)/tpercent, S(8,N)/tpercent, T(N)/Ncubed,
         S(1,N)/Ntolog2of7, S(8,N)/Ntolog2of7);
      N = N*2.0;
   }
}
double T(double N) {
   if (N == 1) return(1);
   else return(8*T(N/2) + 4*(N/2)*(N/2));
}
double S(double lim, double N) {
   if (N <= lim) return(T(N));
   else return(7*S(lim,N/2) + 15*(N/2)*(N/2));
}

Revision date: 2012-09-27. (Please use ISO 8601, the International Standard.)