CS 3343/3341
  Introduction to Algorithms  
  Number Base Conversion   

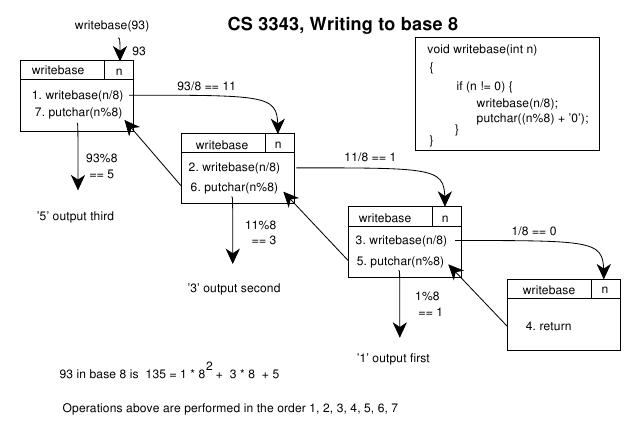
Number Base Conversion: The example below converts a given base 10 number to base 8. (The same technique will work for conversions to any desired base.)

n = 93.  Repeatedly divide by 8 and take the remainder.
         Then repeat with the quotient by 8. Stop at 0 quotient.

93%8 == 5 (remainder) and 93/8 == 11 (quotient)
11%8 == 3 (remainder) and 11/8 ==  1 (quotient)
 1%8 == 1 (remainder) and  1/8 ==  0 (quotient)

The numbers in red boldface (the remainders) are the base 8 digits of 93, generated backwards (least significant digit first). We want to write them forwards, to get 135 (base 8), and for this purpose, we can push them on a stack, and pop them off, as in the following code:

JavaC Language
public void writebase(int n) {
   while (n > 0) {
      push(n%8);
      n = n/8;
   }
   while (!empty())
      System.out.print(pop());
}

void writebase(int n) {
   while (n > 0) {
      push(n%8);
      n = n/8;
   }
   while (!empty())
      printf("%i", pop());
}

Here is complete code to carry out the above program. (The code includes the "simplest possible" stack, to avoid details.)

JavaC Language
// BaseConvert: convert to base 8
public class BaseConvert { 
   public int[] s = new int[100]; // storage for stack
   public int top = 0; // points one above top
   public int pop() { return s[--top]; }//pop, return top
   public void push(int n) { s[top++] = n; } // push item
   public boolean empty() { return top == 0; } // empty?

   public void writebase(int n) {
      while (n > 0) {
         push(n%8);
         n = n/8;
      }
      while (!empty())
         System.out.print(pop());
   }

   public static void main(String[] args) {
      int n = 93;
      BaseConvert baseConvert = new BaseConvert();
      baseConvert.writebase(n);
      System.out.println(" is the value of " +
         n + " (base 8)");
   }
}
// baseconvert.c: convert to base 8
#include <stdio.h>
int s[100]; // storage for the stack
int top = 0; // points one above top
int pop() { return s[--top]; }//pop, return top
void push(int n) { s[top++] = n; } // push item
int empty() { return top == 0; } // empty?

void writebase(int n) {
   while (n > 0) {
      push(n%8);
      n = n/8;
   }
   while (!empty())
      printf("%i", pop());
}

int main() {
   int n = 93;

   writebase(n);
   printf(" is the value of %i (base 8)\n", n);
}

Common Output: 135 is the value of 93 (base 8)

However, there is a much simpler version of the writebase function that uses recursion in place of a stack. Here it is enclosed in a class. It has the same output as the previous program.

JavaC Language
// BaseConversion.java: convert to base 8
public class BaseConversion { 

   public void writebase(int n) {
      if (n != 0) {
         writebase(n/8);
         System.out.print(n%8);
      }
   }

   public static void main(String[] args) {
      int n = 93;
      BaseConversion baseConversion =
         new BaseConversion();
      baseConversion.writebase(n);
      System.out.println(" is the value of " +
         n + " (base 8)");
   }
}

// convert.c: convert to base 8
#include <stdio.h>

void writebase(int n) {
   if (n != 0) {
      writebase(n/8);
      printf("%i", n%8);
   }
}

int main() {
   int n = 93;


   writebase(n);
   printf(" = %i (base 8)\n", n); 
}
 
Output: 135 is the value of 93 (base 8)

Output: 135 = 93 (base 8)

Here's an illustration in the C language of the recursive calls in this specific example. (In this case Java or C makes no difference, except for outputting a digit.) Recursion is implemented using a stack, so you can often expect that recursive calls give the same effect as saving items on a stack.


(Click image for larger version, or here for a PDF.

In the diagram above, the code behaves as if there were a separate function definition for each recursive call. The code below illustrates this:

BaseConversion, With and Without Recursion (both sides are Java)
// BaseConversion: convert to base 8
public class BaseConversion { 

   public void writebase(int n) {
      System.out.println("Enter writebase, n = " + n);
      if (n != 0) {
         writebase(n/8);
         System.out.println("Printing: " + n%8);
      }
      System.out.println("Leave writebase, n = " + n);
   }




























   public static void main(String[] args) {
      int n = 93;
      BaseConversion baseConversion =
         new BaseConversion();
      baseConversion.writebase(n);
      System.out.println(" is the value of " + n +
         " (base 8)");
   }
}

// BaseConversion0: convert to base 8, NO RECURSION
public class BaseConversion0 { 

   public void writebase0(int n) {
      System.out.println("Enter writebase0, n = " + n);
      if (n != 0) {
         writebase1(n/8);
         System.out.println("Printing: " + n%8);
      }
      System.out.println("Leave writebase0, n = " + n);
   }

   public void writebase1(int n) {
      System.out.println("Enter writebase1, n = " + n);
      if (n != 0) {
         writebase2(n/8);
         System.out.println("Printing: " + n%8);
      }
      System.out.println("Leave writebase1, n = " + n);
   }

   public void writebase2(int n) {
      System.out.println("Enter writebase2, n = " + n);
      if (n != 0) {
         writebase3(n/8);
         System.out.println("Printing: " + n%8);
      }
      System.out.println("Leave writebase2, n = " + n);
   }

   public void writebase3(int n) {
      System.out.println("Enter writebase3, n = " + n);
      if (n != 0) {
         writebase0(9999); // not called
         System.out.println("Printing: " + n%8);
      }
      System.out.println("Leave writebase3, n = " + n);
   }

   public static void main(String[] args) {
      int n = 93;
      BaseConversion0 baseConversion0 =
         new BaseConversion0();
      baseConversion0.writebase0(93);
      System.out.println(" is the value of " + n +
         " (base 8)");
   }
}
Output, blue = output of the original program, red = differences from left to right
Enter writebase, n = 93
Enter writebase, n = 11
Enter writebase, n = 1
Enter writebase, n = 0
Leave writebase, n = 0
Printing: 1
Leave writebase, n = 1
Printing: 3
Leave writebase, n = 11
Printing: 5
Leave writebase, n = 93
 is the value of 93, base 8

Enter writebase0, n = 93
Enter writebase1, n = 11
Enter writebase2, n = 1
Enter writebase3, n = 0
Leave writebase3, n = 0
Printing: 1
Leave writebase2, n = 1
Printing: 3
Leave writebase1, n = 11
Printing: 5
Leave writebase0, n = 93
 is the value of 93, base 8

Instead of using a separate copy of recursive functions for each call, programming languages cleverly use a single copy of the machine code for the function, but allocate separate storage on a stack for local variable and parameters, etc. corresponding to each recursive call.

Revision date: 2012-08-29. (Please use ISO 8601, the International Standard Date and Time Notation.)