Introduction to the Design and Analysis of Algorithms
(Textbook. Click for information.)
 CS 3343/3341
 Analysis of Algorithms
 Spring 2012
 Recitation 13
 Final Exam Review
    Week 14: Apr 24-Apr 26
 Due (on time): 2012-05-03  23:59:59
 Due (late):        2012-05-05  23:59:59

Note: As of < Wed May 2 14:40:01 CDT 2012 > the submissions prgram for Recitation 13 is available.
(Sorry for the delay.)

Recitation 13 should be submitted following directions at: submissions with deadlines
  • 2012-05-03  23:59:59 (that's Thursday, 3 May 2012, 11:59:59 pm) for full credit.
  • 2012-05-05  23:59:59 (that's Saturday, 5 May 2012, 11:59:59 pm) for 75% credit.

Notes: 1. The Final Exam is on Monday, 7 May 2012, 10:30-1 pm.
    2. You may bring a single letter-sized sheet of paper to the exam with whatever written on it that you want (but nothing, umm, illegal).

See Online Materials for links to topics covered in the course.

Topics NOT COVERED on the Final Exam. Each of these was covered earlier.

Topics and Review Questions for Final Exam.
  1. Quicksort and Randomization:
    1. Give the algorithm that randomizes the order of the elements in an array. What is it's asymptotic (time) performance?
    2. What is the worst-case asymptotic (time) performance of quicksort?
    3. Explain how you could use Part i above to improve the performance of quicksort. What kind of time performance does this give? What "awkward" input case(s) does this help with? Does this step eliminate these cases altogether? If not, then why and how does this step help?
    4. Explain how the same technique would eliminate some of the same "awkward" input cases if one used a binary search tree for sorting. Also: how would you use a binary search tree for sorting? What kind of performance does this "tree sort" algorithm have?
    5. Your text's Randomized Quicksort is different from Parts i and iii above. Explain the additions to the quicksort algorithm that give Randomized Quicksort.

  2. Dynamic Programming: Not sure if I'll have a problem on this.

  3. Breadth-First and Depth-First Searchs of Graphs: By hand, run through a BFS and a DFS for the graph below, starting with vertex a. Assume that vertices are ordered alphabetically in the adjacency lists. Show the vertices in the order that they are visited. Use a queue (of coures) for BFS and a stack for DFS. (A stack for DFS gives the same order of visits, but not the same finishing times as recursion. I don't care about this here because I'm just asking for the order of the visits. Notice that as you process vertex a in DFS, you will push b and c in that order, so that c will be popped and will be the next vertex processed.) [It is important for you to do this by hand, rather than using your program, as practice for the final. This problem came from C. Wenk.]

    [Answers: For BFS, the order of vertices visited is: a,b,d,c,e,f. For DFS, the order of vertices visited is: a,d,e,f,c,b.]

  4. Graph Representations: Draw the adjaceny list representation for the directed graph in the previous problem. [Annoying to put into text, but this is practice for the final, where it will easy to draw it.]

  5. Dijkstra's Algorithm: By hand, run through Dijkstra's algorithm on the graph below, starting with vertex a. Assume each undirected edge is two directed edges with the same weight in each direction. [As usual, this is awkward to put into text form, but for each stage you can give a line with the vertices still in the priority queue, and the current distance values to each vertex. It is important for you to do this by hand, rather than using your program, as practice for the final. This problem came from C. Wenk.]

  6. Hashing: You had several problems about hashing in Recitation 12.

  7. Reductions Involving Arithmetic Problems: Recall that we looked at 4 problems:

    We also used the relation ≤ to mean "efficient reduction".

    1. Of the two relations, Pm ≤ Ps and Ps ≤ Pm, one of them is trivial, and one depends on the formula:

      Which is which? For the relation that is trivial, why do I call it "trivial"? And for the relation that depends on the formula, explain (briefly) how the formula shows that the relation holds.

    2. Use the formula below and the previous one to argue that: Pm ≤ Pr.

  8. Hamiltonian Cycles:
    1. Give the definition of the Hamiltonian Cycle Problem (HP). (We also called it the Hamiltonian Circuit Problem.)
    2. Does the graph of state capitals have a Hamiltonian Cycle? (Careful here.)
    3. Does a complete graph always have a Hamiltonian cycle?
    4. One of the weird topics (but not Topic 10) talked about proving something involving a Hamiltonian Cycle. What was it?
    5. State the Traveling Salesman Problem (TS).
    6. We proved something involving HC and TS. What was it?
    7. State the Vertex-Cover Problem (VC).
    8. We talked a little about the proof that VC ≤p HC. First of all, what does this formula say about VC and HC? Very roughly (without any details), what must one prove to prove this relation?

  9. Two NP-complete Problems: Subset-Sum and Partition: We already looked at the Subset-Sum Problem (Recitation 7), but the notation below is slightly different than before:

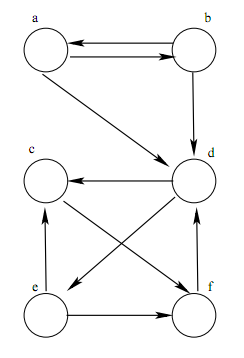
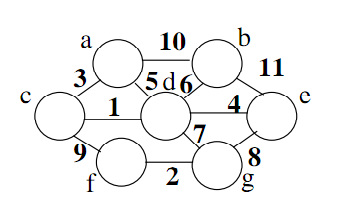
    Subset-Sum Problem (SS):
    Start with a set A of positive integers and a desired sum S.
    The decision question: Is there a subset A' of A such that sum( a | a in A' ) = S?

    Next is the Parition Problem (PART):

    Partition Problem (PART):
    Start with a set A of positive integers.
    The decision question: Is there a subset A' of A such that
    sum( a | a in A' ) =  sum( a | a in A - A' )?
    [Here A - A' is the complement of A' in A.]

    Show that PART ≤p SS, that is, show that PART can be reduced to SS.

    [Hints: You need to start with an arbitrary problem in PART. Then come up with a way to transform any problem P in PART into a problem P' in SS. Finally show that the answer is "Yes" to P if and only if (exactly when) the answer is "Yes" to P'.]

  10. Turing Machines, Undecidable Problems: Consider the following "mystery" program in the language used for our Turing machines:

    Instructions in the Turing Language
    InstructionRepresentation Op
    Code
    print 0 000 0
    print 1 001 1
    move left 010 2
    move right 011 3
    stop 100 4
    if 0 is scanned
     goto i    		 101 0...0 1
        <-i->    		 5
    if 1 is scanned
     goto j    		 110 1...1 0
        <-j->    		 6
    (end marker) 111 -
    		 
    Mystery Program ??
    InstructionRepresentation
     1. move left
 2. if 1 is scanned goto 1
 3. if 0 is scanned goto 4
 4. print 1
 5. move right
 6. if 1 is scanned goto 5
 7. print 1
 8. move right
 9. if 0 is scanned goto 1
10. stop
    (end)

Initial   ...0000000000...
 tape:           |

    010
110 1 0
101 0000 1
001
011
110 11111 0
001
011
101 0 1
100
111

    1. Explain carefully what this mystery program does. What is its output and what actions does it go through to produce this output? (This is easier than you might think, although in a sense it's a bit of a trick.)
    2. Three of the instructions in this program can be replaced by a single instruction in such a way that the resulting program still prints 1's on the tape in the same places and in the same order. Can you figure out which 3 instructions could be replaced by one instruction? (Also a bit of a trick.)

  11. All "sufficiently powerful" models of computation known up to now have equivalent computing power. These are called Turing Complete. They include all the normal programming languages and all the usual computers. The Church-Turing Thesis is the axiom (or hypothesis) that no more powerful model can exist. But common models are not Turing complete. Take for example the Finite Automata (FA) (aka Finite-State Machines). The rule is: "FAs can't count." A given FA isn't even powerful enough to count to an arbitrary number. An FA equiped with a stack (called a "Push-down Automaton) can count, but it still isn't complete.

    Usually we want our programming languages to have lots of nice and powerful instructions so that they are easy to program -- so that we can write short but powerful programs. OK, finally here is the question: Why did Turing make his machine as simple as possible? Why are the other Turing machines also simple like this and almost impossible to program? What's the advantage of being so simple?

  12. Write a short essay on the theological implications of the Game of Life. Just kidding, although some of these issues are explored in many places on the net, for example, Simulated Evolution.

Revision date: 2012-04-27. (Please use ISO 8601, the International Standard.)