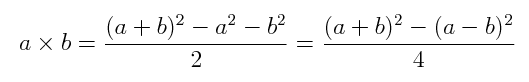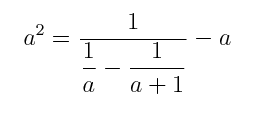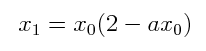(Textbook. Click for information.)

CS 3343/3341  Analysis of Algorithms  Spring 2012  Recitation 12  Hashing, Reductions     Week 13: Apr 17-Apr 19  Due (on time): 2012-04-25  23:59:59  Due (late):        2012-04-27  23:59:59

Recitation 12 should be submitted following directions at: submissions with deadlines 2012-04-25  23:59:59 (that's Wednesday, 25 April 2012, 11:59:59 pm) for full credit. 2012-04-27  23:59:59 (that's Friday, 27 April 2012, 11:59:59 pm) for 75% credit.

Note: As of < Sat Apr 21 22:47:31 CDT 2012 > I put up the submission program for this recitation and tested it.

---

1. Look at the writeup Zero-Knowledge Proofs and in particular at the table on page 146.
   1. Give simple pseudo-code showing how anyone could prove that the "Cycle" column represents a Hamiltonian cycle. (This should be an algorithm not using pictures.)
   2. Is your algorithm polynomial time?
   3. Assuming that it is, what does this fact alone say about the status of the problem Hamiltonian cycle?
   4. What data does Alice show to Bob in case he asks to see the Hamiltonian cycle?
   5. How many trials would Bob need to give him at least 99.9% confidence that Alice is not cheating?

   ---

2. Hashing
   1. Suppose you are using the hash function hash(anything) = 3, which returns 3 no matter what the input. Explain what happens with both chaining and with open addressing in this case.

   2. Suppose you use hashing with open addressing in a table of size m. Explain what happens as you insert m items into this table. (This assumes a normal hash function, rather than the function in part (i) above.)

   3. The Birthday Paradox asks how many people with random birthdays does it take to have better than even odds that at least two have the same birthday (same month and same day). (This is ignoring February 29.)

      It is easier to calculate the probability that among n people, no two have the same birthday. Denote this by N(n). For two people, the second one will have a birthday different from the first with probability:
              N(2) = 364/365.
      If there is a third person the probability that he will have a birthday different from the first two (which are assumed distinct now), is 363/365, so that
              N(3) = (364/365)*(363/365).
      Similarly,
              N(4) = (364/365)*(363/365)*(362/365).
      Of course, N(1) = 1.

      The probability, call it S(n), that at least two people from among n have the same birthday is just:
              S(n) = 1 - N(n).

      Write a simple program that will calculate and print S(n) for n = 1, 2, 3, ..., 50. These should be calculated as doubles.

   4. What does Part iii of this exercise say about using open addressing to insert into a hash table of size 365?

---

3. Reductions Suppose you are writing software for a high-precision floating point engine. (Instead of 64-bit floating point numbers, perhaps 1024-bit fp numbers -- most of these used for the significant part, and the remainder for the sign and exponent.) Suppose you have written reasonably efficient addition, subtraction, and negation routines for these number, and you can also efficiently multiply and divide by powers of 2. Now you want to add other arithmetic functions, especially multiplication and division.

   We will look at 4 problems:

   P_m = multiplication of two numbers (a* b)
   P_d = division of two numbers (a/b)
   P_r = reciprocal of a number (1/a)
   P_s = square of a number (a²)
   

   We will be writing stuff like P₁ ≤ P₂ to mean a reduction of P₁ to P₂, similar to the book's ≤_p. However, here it's not polynomial-time, but rather an efficient reduction comparable to the other operations on these numbers. Intuitively, this means: if you can compute P₂ efficiently, then you can compute P₁ efficiently.

   1. If 1000 binary bits are used for the significant part, roughly how many decimal digits of accuracy would we have?

   2. Explain why it is trivial to see that P_s ≤ P_m

   3. Use the formula below (with either part on the right) to show that P_m ≤ P_s
      

   4. Use the formula below to show that P_s ≤ P_r
      

   5. Recall that we used the following iteration formula from Newton's method to find the reciprocal. Argue that this shows that P_r ≤ P_m [Note: Until Tuesday morning this was written P_d ≤ P_m in error.]
      

      You should explain in some detail how you intend to handle the initial guess for Newton's method, which should not be too far from the correct answer.

   6. Argue that if you can do both P_m and P_r efficiently, then you can also do P_d efficiently.

   7. Explain why if we can do P_s efficiently, then we can also do the other three efficiently: P_m, P_r, and P_d. (This would be a quick and dirty way to do a half-way efficient implementation.) [Note: Part iv above is just an extra fact that shows that P_m, P_r, and P_s are equivalent. Part iv is not needed to show this part vii.]