Textbook.

CS 3343  Analysis of Algorithms  Fall 2012  Recitation 14   Final Review      Week 14: Dec 4-Dec 6  Due (on time): 2012-12-10  23:59:59  Due (late):        2012-12-11  22:00:00

Topics NOT COVERED on the Final Exam.

• Induction proofs.
• The slow and quick exponentiation algorithms.
• Quicksort and finding the median with a variation of quicksort.
• Heaps, heapsort, and use of heaps to create a priority queue. (But you might need to know what a priority queue is.)
• Random number generators, randomization.

---

1. Use the Master Theorem to analyze each of the following recurrences. (The theorem may not work for some of them.)
   1. T(n) = 64 T(n / 4) + √n

   2. T(n) = 9 T(n / 3) + n² log(n)

   3. T(n) = 16 T(n / 4) + n⁴

   4. T(n) = 2 T(n / 4) + √n

   ---

2. Strassen's Method for Matrix Multiplication:
   1. Consider the matrix multiplication of 4-by-4 matrices.
      1. Using the ordinary method of matrix multiplication, how many scalar multiplications are required? Don't just state this number, but calculate the number from the ordinary matrix multiplication algorithm, where each element of the answer is the inner product of a length 4 row times a length 4 column.

      2. Using the divide-and-conquer approach and Strassen's method of multiplying 2-by-2 matrices, how many scaler multiplications would be required? Again justify your answer.

   2. Now consider 5-by-5 matrices. Again how many scalar multiplications would be required using ordinary matrix multiplication? (Just a number for the answer.) Suppose one could multiply 5-by-5 matrices using 91 scalar multiplications. Give the recurrence for a divide-and-conquer algorithm based on this supposition. Use the Master Method (or some other approach) so get the asymptotic performance in this case. Would this be an interesting result?

   ---

3. Dijkstra's Algorithm: Refer to Problem 4 in Recitation 13 and its answer, along with the other sample problems.

   ---

4. Breadth-First and Depth-First Searches of Graphs: By hand, run through a separate BFS and a separate DFS for the graph below, starting with vertex a. Assume that vertices are ordered alphabetically in the adjacency lists. Show the vertices in the order that they are visited. For each search you must use a stack or a queue, whichever is appropriate, but should not use recursion for this problem. Show the insertions and removals for each case. In each case the sequence of removals should be your final answer. (You don't need to gather any of the other information that was obtained when we did graph searches.)
   

   ---

5. Example of Polynomial Time Equivalence. Consider the two problems:
   L₁: find the square root of x, where 1/4 <= x <= 1.
   L₂: find the square root of x, where 0 < x.

   Consider also the two reductions L₁ ≤_p L₂ and L₂ ≤_p L₁.

   1. One of these reductions is trivial. Which one is "trivial" and why do I use that word.?
   2. The other is something that we proved. What rough technique did we use to prove it?

   ---

6. Problems in NP: This problem has nothing to do with NP-complete problems, but just NP.
   1. Is any problem in P (polynomial-time problems) also in NP?
   2. Is P the same as NP? Can you prove this?
   3. Give the "guessing-stage / checking-stage" definition that shows a problem is in NP.
   4. How would you use the definition in (iii) above to show that the problem Subset Sum (SS) is in NP? Here you start with a set A of positive integers and a given sum S. The problem is whether or not A has a subset A' whose numbers add up to S.

   ---

7. Two NP-complete Problems: Subset-Sum and Partition: We already looked at the Subset-Sum Problem (Recitation 7), but the notation below is slightly different than before:

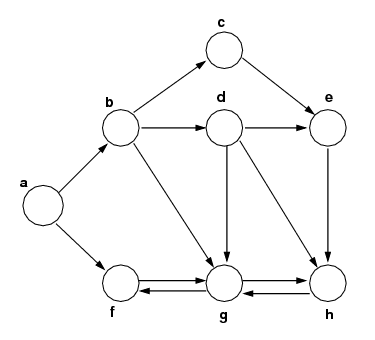
   Subset-Sum Problem (SS): Start with a set A of positive integers and a desired sum S. The decision question: Is there a subset A' of A such that sum( a | a in A' ) = S?

   Next is the Parition Problem (PART):

   Partition Problem (PART): Start with a set A of positive integers. The decision question: Is there a subset A' of A such that sum( a | a in A' ) =  sum( a | a in A - A' )? [Here A - A' is the complement of A' in A.]

   Show that PART ≤_p SS, that is, show that PART can be reduced to SS.

   Which of the two following facts does this prove:

   a. If PART is NP-complete then SS is NP-complete, or
   b. If SS is NP-complete then PART is NP-complete.

   [Hints: We will go over in class what you need to start with and what you need to prove.]

   ---

8. Turing Machines, Undecidable Problems: Consider the following "mystery" program in the language used for our Turing machines:

   Instructions in the Turing Language Instruction Representation Op Code print 0 000 0 print 1 001 1 move left 010 2 move right 011 3 stop 100 4 if 0 is scanned  goto i 101 0...0 1     <-i-> 5 if 1 is scanned  goto j 110 1...1 0     <-j-> 6 (end marker) 111 -

   Mystery Program ?? Instruction Representation 1. move left 2. if 1 is scanned goto 1 3. if 0 is scanned goto 4 4. print 1 5. move right 6. if 1 is scanned goto 5 7. print 1 8. move right 9. if 0 is scanned goto 1 10. stop (end) Initial ...0000000000... tape: | 010 110 1 0 101 0000 1 001 011 110 11111 0 001 011 101 0 1 100 111

   Explain carefully what this mystery program does. What is its output and what actions does it go through to produce this output? (This is easier than you might think, although in a sense it's a bit of a trick.)