CS3343, Spring 2012, Quiz 3, 24 April 2012, Answers                      Your Name:                                      

  1. In your text's algorithms for breadth-first and depth-first search, each vertex at various stages had one of three colors: white, gray, or black. With one line of explanation for each color, explain how the color is used by the algorithm or what specifically the different colors indicate.

      White: Initial color, before "discovered" or referenced.
      Gray: When first "discovered" or referenced, change to this color. Stays Gray as long as active in algorithm.
      Black: As last activity with a vertex, change to Black. Vertex is "finished".

  2. The algorithm for breadth-first search manages to visit all vertices near the starting vertex, before moving further away. How is this managed? In other words, why doesn't the algorithm just wander away from the starting vertex without visiting all nearby vertices? (Short answer.) First the start vertex and then vertices on its adjacency list are put into a (first-in, first-out)queue. Then vertices on further adjacency lists are put in the queue. Thus the vertices are processed in the order they went in: first the start vertex, then vertices on its adjacency list, etc. The algorithm doesn't get to further adjacency lists until the earlier ones are completely processed.

  3. Consider the directed graph below:

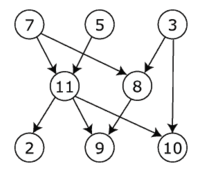    Use the "Alternative Method" of carrying out a topological sort given at the end of Recitation 10: "Another way to perform topological sorting on a directed acyclic graph is to repeatedly find a vertex of in-degree 0, output it, and remove it and all its outgoing edges from the graph." For full credit, it is not enough to display a topological sort, but you must show (more or less) that you are using the method in quotation marks. This is kind of a silly and obvious problem. Sorry.

  4. Suppose you are finding log2(t) where t=13 as we did in the first part of Recitation 11. Suppose you first want to normalize t=13 into the interval from 1 to 2 inclusive. What operation(s) would you perform on this value of t to produce t' satifying 1 <= t' <= 2? After finding log2(t'), what operation(s) would you perform on the result to get the desired value log2(13). (Just two very short answers are all you need here: what you do to 13 to normalize, and what you do at the end to denormalize.) OK, we divide t=13 by a power of 2 to normalize, in this case divide by 23 to get t'=t/8=1.625. (Of course we could just as well say that we are multiplying by 2-3.) Then somehow find log2(t') = log2(t / 23) = log2(t) - log2(23) = log2(t) - 3. Thus log2(t) = log2(t / 23) + 3. So the normalization in this case is to divide by 23 = 8 and the denormalization is to add 3.

    For reference, log2(t') = log2(1.625) = 0.7004397, so this says that log2(t) = log2(1.625) + 3 = 0.7004397 + 3 = 3.7004397. A separate calculation shows that this is the correct value of log2(13).