Click box or here for full size image.
CS 3343 Analysis of Algorithms Weird Topic |
Bin Packing
Approximation |
| Bin-Packing Problem (BP): Start with a positive integer bin size denoted by W, and a finite set of positive integers {b1, b2, ...} which are item sizes of items to packed into a succession of bins. A bin packing is an assignment of each each item to a bin in such a way that the sum of the item sizes for items in each bin is less than or equal to W. The decision question is: Given an integer k, is there a bin-packing using k bins? |
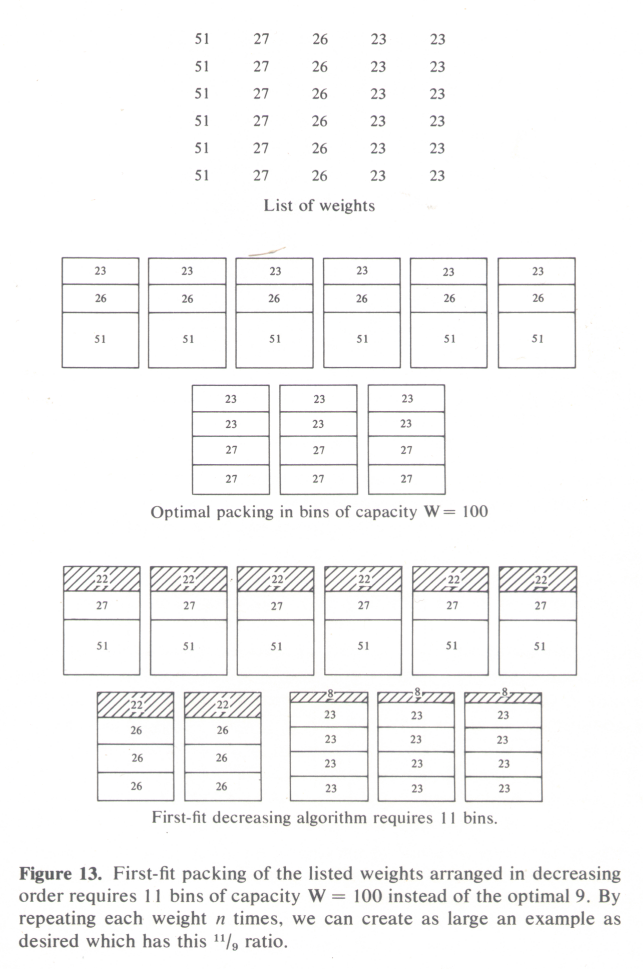
| First Fit (FF) Approximation Algorithm: Start with the items in an arbitrary order, perhaps their order of occurrence, and with an ordered sequence of empty bins. Place each successive item into the first bin into which it will fit. Check if the number of non-empty bins is less than or equal to k. |

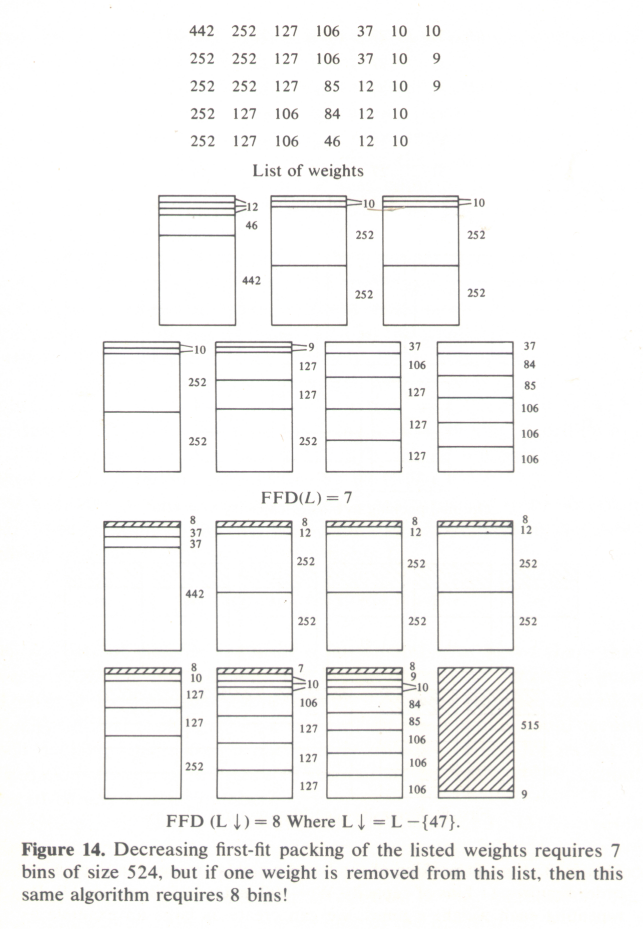
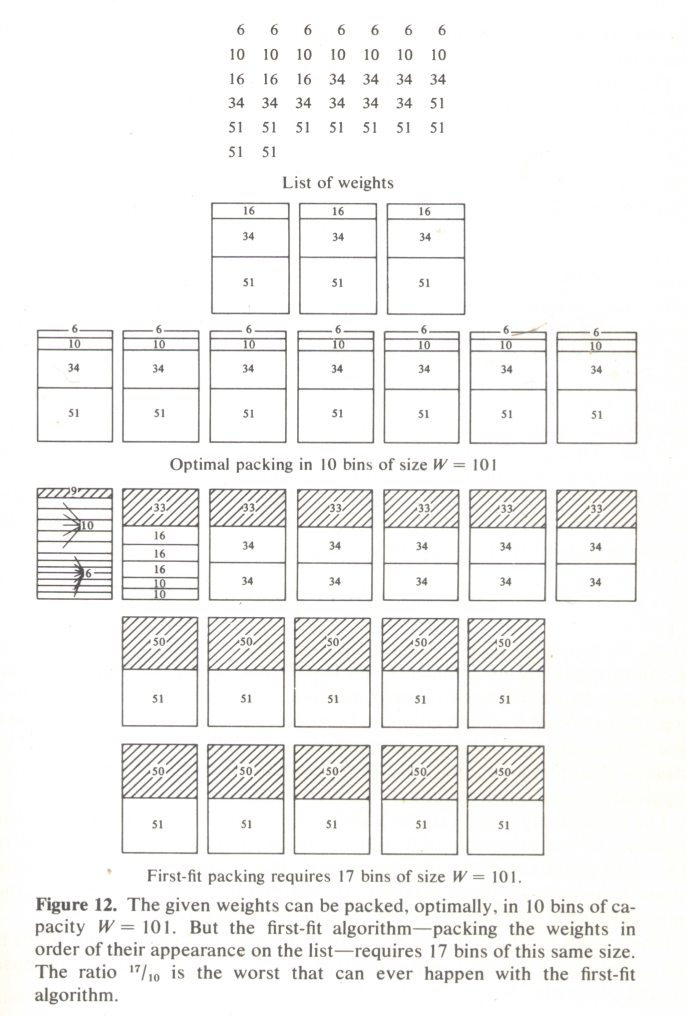
| First Fit Decreasing (FFD) Approximation Algorithm: The same as FF, except that we start with the items in non-increasing order. |