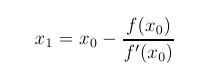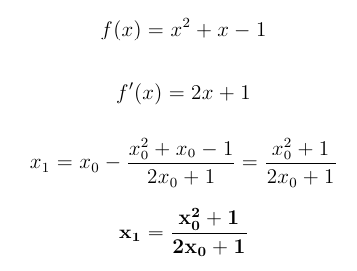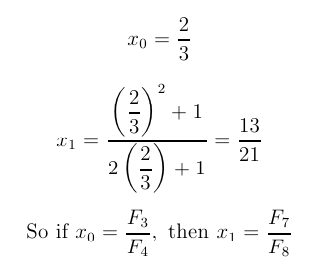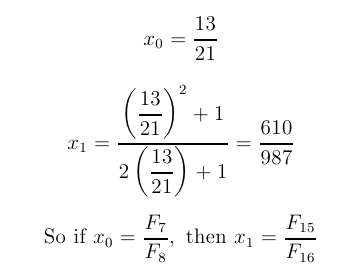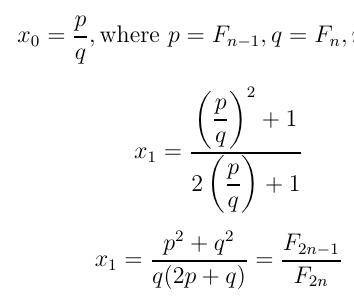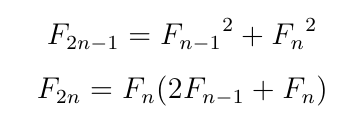CS3343/3341
Analysis of Algorithms
Spring 2012
Weird Topic |
Newton's Method, Part 2
The Golden Ratio and
Fibonacci Formulas
|
The Golden Ratio:
The golden mean or golden ratio,
denoted by φ, is the ratio a / b of
the lengths of two sides of the rectangle below:
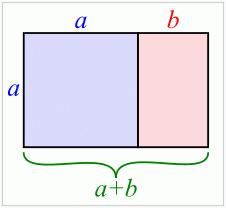 The definition of φ says that the
ratio of sides of the smaller rectangle to the left must be the
same as that of the large rectangle:
(a + b) / a = a / b = φ.
Set b = 1 to get
(a + 1) / a = a = φ.
Then φ is the positive root of
a2 - a - 1 = 0,
which is
φ = (1 + sqrt(5)) / 2
= 1.61803 39887 49894 84820 45868 ...
Formulas involving φ are:
(φ + 1) / φ = φ
and φ - 1 = 1 / φ
1 / φ = (sqrt(5) - 1) / 2
= 0.61803 39887 49894 84820 45868 ...
Also, Fn+1 / Fn converges
to φ as n tends to infinity, and
Fn / Fn+1 converges
to 1 / φ as n tends to infinity.
The definition of φ says that the
ratio of sides of the smaller rectangle to the left must be the
same as that of the large rectangle:
(a + b) / a = a / b = φ.
Set b = 1 to get
(a + 1) / a = a = φ.
Then φ is the positive root of
a2 - a - 1 = 0,
which is
φ = (1 + sqrt(5)) / 2
= 1.61803 39887 49894 84820 45868 ...
Formulas involving φ are:
(φ + 1) / φ = φ
and φ - 1 = 1 / φ
1 / φ = (sqrt(5) - 1) / 2
= 0.61803 39887 49894 84820 45868 ...
Also, Fn+1 / Fn converges
to φ as n tends to infinity, and
Fn / Fn+1 converges
to 1 / φ as n tends to infinity.
Calculate φ - 1 = 1 / φ:
Recall from a previous page that Newton's Method
is used to find successive approximations to
the roots of a function. If the function is y = f(x)
and x0 is close to a root, then we usually
expect the formula below to give x1
as a better approximation. Then you plug the x1
back in as x0 and iterate.
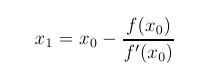 In this case we are using the equation for 1 / φ,
namely
x2 + x - 1 = 0.
(Everything below would also work if we started with the
equation for φ instead.)
In this case we are using the equation for 1 / φ,
namely
x2 + x - 1 = 0.
(Everything below would also work if we started with the
equation for φ instead.)
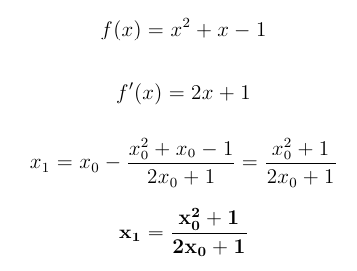 If we plug x0 = 1 into the above
equation, we get x1 = 2 / 3.
Now iterate with x0 = 2 / 3.
If we plug x0 = 1 into the above
equation, we get x1 = 2 / 3.
Now iterate with x0 = 2 / 3.
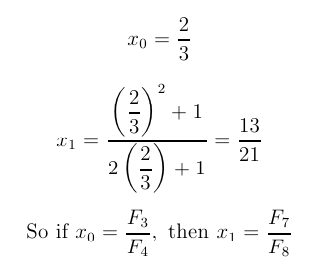 There are a lot of Fibonacci numbers floating around here.
Try one more iteration:
There are a lot of Fibonacci numbers floating around here.
Try one more iteration:
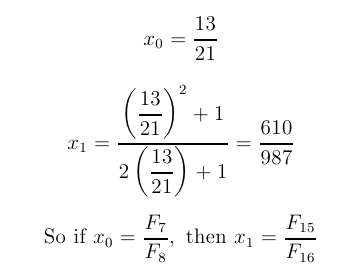 In general, start with p / q, where these
are successive Fibonacci numbers,
Fn-1 / Fn.
In general, start with p / q, where these
are successive Fibonacci numbers,
Fn-1 / Fn.
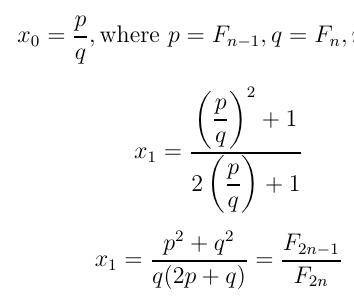 So the same formulas for Fibonacci numbers that we got earlier
from matrices are falling out from Newton's method:
So the same formulas for Fibonacci numbers that we got earlier
from matrices are falling out from Newton's method:
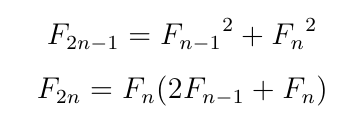
Revision date: 2011-12-05.
(Please use ISO 8601,
the International Standard Date and Time Notation.)