CS 3343/3341
 Analysis of Algorithms 
Spring 2012
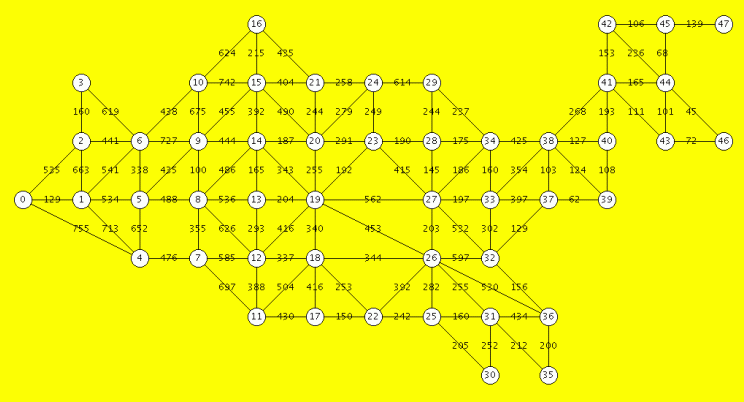
  Graph of Capitals in USA   

This graph, along with its elegant layout, is due to Donald Knuth, who used it in a number of places in his Vol. 4. The picture above was not created by the program below. Instead, this program gives a framework for creating a graph data structure in Java. The program's output is at the end of this webpage.

In order to simplify the code, I removed the accessor methods from my original code and made the data members public.

The specific graph here gives distances between capital cities in the continental US. For the two-letter name of each capital's state, see here.

Graph construction: 48 mainland US capitals. Data from file: capsdistnum.txt
// Graph.java: set up data structure for graph
//  Uses adjacency list representation
import java.io.*;
import java.util.Scanner;
public class Graph {
   private int count; // number of nodes
   private Scanner sc; // input file name
   private GraphNode[] graph;

   private void err(int code) {
      System.exit(code);
   }

   public Graph(String fileName, int ct) {
      count = ct;
      int num1 = 0, num2 = 0, num = 0;
      graph = new GraphNode[count];
      for (int i = 0; i < count; i++)
         graph[i] = null;
      try {
         sc = new Scanner(new
            File("capsdistnum.txt"));
      }
      catch (Exception exception ) { err(1); }
      while (sc.hasNextInt()) {
         num1 = sc.nextInt();
         if (sc.hasNextInt())
            num2 = sc.nextInt();
         else err(2);
         if (sc.hasNextInt())
            num = sc.nextInt();
         else err(3);
         // carry out insertions, both directions
         insert(num1, num2, num);
         insert(num2, num1, num);
     }
   }

   private void insert(int num1, int num2,
           int dist) {
      // patch the new node in at the start
      GraphNode node = graph[num1];
      if (node == null) {
         GraphNode gnode = new GraphNode();
         graph[num1] = gnode;
         EdgeNode enode = new EdgeNode(num2, null,
            dist);
         graph[num1].firstEdgeNode = enode;
      }
      else {
         EdgeNode enode = new EdgeNode(num2,
            graph[num1].firstEdgeNode, dist);
         graph[num1].firstEdgeNode = enode;
      }
   }

   public void printGraph() {
      for (int i = 0; i < count; i++) {
         System.out.print(i + ": ");
         EdgeNode node = graph[i].firstEdgeNode;
         while (node != null) {
            System.out.print("[" + node.vertexNum +
               "," + node.edgeDist + "]");
            node = node.nextEdgeNode;
            if (node != null)System.out.print(",");
            else System.out.print("\n");
         }
      }
   }
}

// GraphNode.java: node for graph's vertex
//  Holds vertex info, link to adj. list
public class GraphNode {
   public EdgeNode firstEdgeNode;
   // other vertex info here

   public GraphNode() {
      firstEdgeNode = null;
      // initialize other vertex info here
   }
}

// EdgeNode.java: holds graph's edge info
//  Implement adjacency list
public class EdgeNode {
   public int vertexNum; // vertex num
   public EdgeNode nextEdgeNode;//next node
   public int edgeDist; // edge length
   // other edge info here

   public EdgeNode(int num, EdgeNode node,
         int dist) {
      vertexNum = num;
      nextEdgeNode = node;
      edgeDist = dist;
      // initialize other edge info here
   }
}

// GraphMain.java: Controls Graph Program
import java.io.*;
public class GraphMain {
   public static void main(String[] args) {
       final int GRAPHSIZE = 48;
       Graph graph = new Graph(
             "capsdistnum.txt", GRAPHSIZE);
       graph.printGraph();
   }
}
Pairs of Cities with Distances
(Edges and weights)
file: capsdistnum.txt
0  4 755
0  1 129
0  2 535
1  4 713
1  5 534
1  6 541
1  2 663
2  6 441
2  3 160
3  6 619
4  7 476
4  5 652
5  8 488
5  9 435
5  6 338
6  9 727
6 10 438
7 11 697
7 12 585
7  8 355
8 12 626
8 13 536
8 14 486
8  9 100
9 14 444
9 15 455
9 10 675

10 15 742
10 16 624
11 17 430
11 18 504
11 12 388
12 18 337
12 19 416
12 13 293
13 19 204
13 14 165
14 19 343
14 20 187
14 15 392
15 20 490
15 21 404
15 16 215
16 21 435
17 22 150
17 18 416
18 22 253
18 26 344
18 19 340
19 26 453
19 27 562
19 23 192
19 20 255

20 23 291
20 24 279
20 21 244
21 24 258
22 25 242
22 26 392
23 27 415
23 28 190
23 24 249
24 29 614
25 30 205
25 31 160
25 26 282
26 31 255
26 36 530
26 32 597
26 27 203
27 32 532
27 33 197
27 34 186
27 28 145
28 34 175
28 29 244
29 34 237
30 31 252
31 35 212

31 36 434
32 36 156
32 37 129
32 33 302
33 37 397
33 38 354
33 34 160
34 38 425
35 36 200
37 39 62
37 38 103
38 39 124
38 40 127
38 41 268
39 40 108
40 41 193
41 43 111
41 44 165
41 42 153
42 44 236
42 45 106
43 46 72
43 44 101
44 46 45
44 45 68
45 47 139

Complete Structure of the Internal Graph Representation
(undirected graph, so each edge appears twice)
First
vertex		Second vertices of edges and distances,
starting with the first vertex at the left
0: [2.535],[1.129],[4.755]
1: [2.663],[6.541],[5.534],[4.713],[0.129]
2: [3.160],[6.441],[1.663],[0.535]
3: [6.619],[2.160]
4: [5.652],[7.476],[1.713],[0.755]
5: [6.338],[9.435],[8.488],[4.652],[1.534]
6: [10.438],[9.727],[5.338],[3.619],[2.441],[1.541]
7: [8.355],[12.585],[11.697],[4.476]
8: [9.100],[14.486],[13.536],[12.626],[7.355],[5.488]
9: [10.675],[15.455],[14.444],[8.100],[6.727],[5.435]
10: [16.624],[15.742],[9.675],[6.438]
11: [12.388],[18.504],[17.430],[7.697]
12: [13.293],[19.416],[18.337],[11.388],[8.626],[7.585]
13: [14.165],[19.204],[12.293],[8.536]
14: [15.392],[20.187],[19.343],[13.165],[9.444],[8.486]
15: [16.215],[21.404],[20.490],[14.392],[10.742],[9.455]
16: [21.435],[15.215],[10.624]
17: [18.416],[22.150],[11.430]
18: [19.340],[26.344],[22.253],[17.416],[12.337],[11.504]
19: [20.255],[23.192],[27.562],[26.453],[18.340],[14.343],[13.204],[12.416]
20: [21.244],[24.279],[23.291],[19.255],[15.490],[14.187]
21: [24.258],[20.244],[16.435],[15.404]
22: [26.392],[25.242],[18.253],[17.150]
23: [24.249],[28.190],[27.415],[20.291],[19.192]
24: [29.614],[23.249],[21.258],[20.279]
25: [26.282],[31.160],[30.205],[22.242]
26: [27.203],[32.597],[36.530],[31.255],[25.282],[22.392],[19.453],[18.344]
27: [28.145],[34.186],[33.197],[32.532],[26.203],[23.415],[19.562]
28: [29.244],[34.175],[27.145],[23.190]
29: [34.237],[28.244],[24.614]
30: [31.252],[25.205]
31: [36.434],[35.212],[30.252],[26.255],[25.160]
32: [33.302],[37.129],[36.156],[27.532],[26.597]
33: [34.160],[38.354],[37.397],[32.302],[27.197]
34: [38.425],[33.160],[29.237],[28.175],[27.186]
35: [36.200],[31.212]
36: [35.200],[32.156],[31.434],[26.530]
37: [38.103],[39.62],[33.397],[32.129]
38: [41.268],[40.127],[39.124],[37.103],[34.425],[33.354]
39: [40.108],[38.124],[37.62]
40: [41.193],[39.108],[38.127]
41: [42.153],[44.165],[43.111],[40.193],[38.268]
42: [45.106],[44.236],[41.153]
43: [44.101],[46.72],[41.111]
44: [45.68],[46.45],[43.101],[42.236],[41.165]
45: [47.139],[44.68],[42.106]
46: [44.45],[43.72]
47: [45.139]

Revision date: 2011-10-05. (Please use ISO 8601, the International Standard Date and Time Notation.)