CS 3343, Final Exam

CS3343, Fall 2012, Final Exam, 13 Dec 2012		Your Name:
			Last		First

Directions: Do not spend too much time on any one problem. Try to give as short an answer as you can that still fully answers the question.

(20) Use the Master Theorem to analyze each of the following recurrences. (The theorem may not work for some of them.)
1. T(n) = 32 T(n / 2) + n²
2. T(n) = 2 T(n / 4) + √n log(n)
3. T(n) = 2 T(n / 2) + n²
4. T(n) = 16 T(n / 4) + n²

(10) Strassen's Method for Matrix Multiplication: Consider multiplication of 5-by-5 matrices.

How many scalar multiplications would be required to multiply 5-by-5 matrices using ordinary matrix multiplication? (Justify your answer.)
Suppose one could multiply 5-by-5 matrices using 91 scalar multiplications. Give the recurrence for a divide-and-conquer algorithm that would use this fact to multiply matrices of size n-by-n where n is a power of 5.
Use the Master Method (or some other approach) so get the asymptotic performance in this case. (You may leave the answer in terms of logarithms.)

(25) Breadth-First and Depth-First Searches of Graphs: By hand, run through a BFS and a DFS for the graph below, starting with vertex a. Assume that vertices are ordered alphabetically in the adjacency lists. Show the vertices in the order that they are visited. For each search you must use a stack or a queue, whichever is appropriate, but should not use recursion for this problem.

(25) Dijkstra's Algorithm: Here is a graph to which you should apply Dijkstra's algorithm by hand. This includes deciding on the predecessor of each vertex (= node) as well as the distance from the source vertex (the pi and d fields). In this example the nodes are named (s, a, b, ...) rather than numbered. The source vertex is s. You should fill in each square in the table beside the graph with the currenct integer distance and the current predessor vertex. (You can also give your answer in another way, without the table, but you must be sure to show intermediate steps, especially the relax steps.)

Action	Contents of Priority Queue (* = removed)
Remove & Relax	s	a	b	c	d
Initial	0, nil	∞, nil	∞, nil	∞, nil	∞, nil

(10) Adjacency List: Sketch a picture of the internal adjacency list representation of the graph in problem 4 above.
(30) Alternative Topological Sort (using the vertex in-degree) [From your text, page 615] "Another way to perform topological sorting on a directed acyclic graph G = (V, E) is to repeatedly find a vertex of in-degree 0, output it, and remove it and all its outgoing edges from the graph. Explain how to implement this idea so that it runs in time O(V + E). What happens to this algorithm if G has cycles?" Here "in-degree" of a given vertex means the number of edges coming into the vertex. For example, in the graph below, vertex m has in-degree 0 (no edges coming in), while q has in-degree 2 (2 edges coming in; the number of edges going out makes no difference).
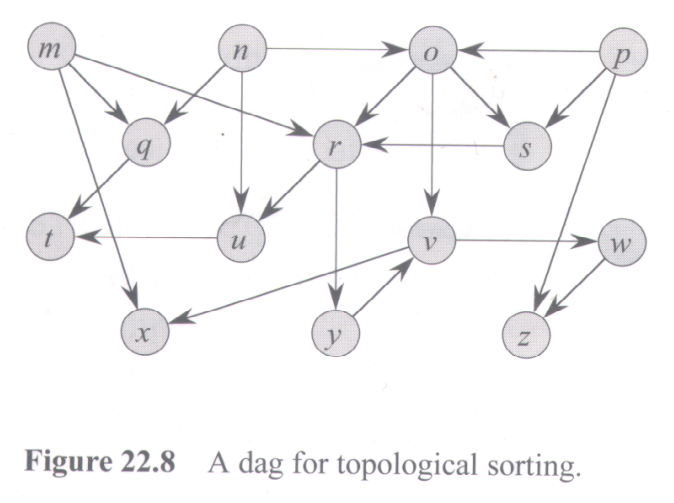
1. First carry out this algorithm by hand on the dag above. [Hint: make a list of the vertices, from m to z. Beside or below each vertex, write its in-degree. Now each time you remove a vertex (call it k) with in-degree 0, "remove" its edges heading out by lowering the in-degree of each target vertex at the end of an edge from k. The topological sort is the list of vertices in the order removed.]
2. What will happen if the graph has a cycle, and therefore has no topological sort? (How will the algorithm behave if there is a cycle?)
3. Describe an efficient way to calculate the in-degrees of all vertices at the start of an algorithm. (This can be done in O(V + E) time.) Argue that the whole algorithm will be O(V + E). (This means that there is a fixed constant c so that the time will be less than c * (V + E) for all graphs.
(20) Reductions Involving Arithmetic Problems: Recall that we looked at 4 problems:
We also used the relation ≤ to mean "efficient reduction".
1. Of the two relations, P_m ≤ P_s and P_s ≤ P_m, one of them is trivial, and one depends on the formula:
  
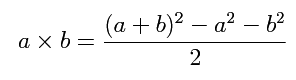
  Which is which? For the relation that is trivial, why do I call it "trivial"? And for the relation that depends on the formula, explain (briefly) how the formula shows that the relation holds.
2. Use the formula below and the previous one to argue that: P_m ≤ P_r.

(20) Turing Machine: Consider the following "mystery" program in the language used for our Turing machines:

Instructions in the Turing Language
Instruction	Representation	Op Code

`print 0`	`000`	`0`
`print 1`	`001`	`1`
`move left`	`010`	`2`
`move right`	`011`	`3`
`stop`	`100`	`4`
`if 0 is scanned goto i`	`101 0...0 1 <-i->`	`5`
`if 1 is scanned goto j`	`110 1...1 0 <-j->`	`6`
`(end marker)`	`111`	`-`

Mystery Program ??

Instruction

Representation

 1. print 0
 2. move right
 3. if 1 is scanned goto 2
 4. print 1
 5. move left
 6. if 1 is scanned goto 5
 7. move left
 8. if 0 is scanned goto 7
 9. print 0
10. move left
11. if 1 is scanned goto 10
12. print 1
13. move right
14. if 1 is scanned goto 13
15. move right
16. if 0 is scanned goto 15
17. if 1 is scanned goto 1
18. stop
    (end marker)

Initial   ...0001100011000...
 tape:               |

000
011
110 11 0
001
010
110 11111 0
010
101 0000000 1
000
010
110 1111111111 0
001
011
110 1111111111111 0
011
101 000000000000000 1
110 1 0
100
111

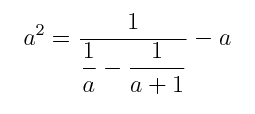
Explain carefully what this mystery program does. What is its output and what actions does it go through to produce this output? (All tape squares outside those shown are zero.)
Explain what the program would do if the starting tape configuration were the following:
Initial ...00011100111000... tape: |

(10) Example of Polynomial Time Equivalence. Consider the two problems:
Consider also the two reductions L₁ ≤_p L₂ and L₂ ≤_p L₁.
1. One of these reductions is trivial. Which one is "trivial" and why do I use that word.?
2. The other is something that we proved. What rough technique did we use to prove it?
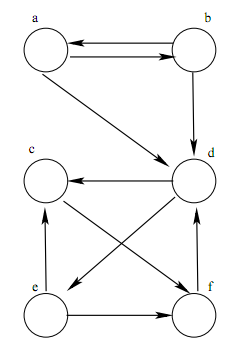
(10) Hamiltonian Cycles and Paths: Recall that a Hamiltonian Cycle (HC) is a path in an undirected graph that includes all vertices exactly once, and starts and ends at the same vertex. A Hamiltonian Path (HP) is a path that also includes all vertices exactly once, but it starts and ends at distinct vertices. (In this notation, an HC is not an HP, because an HC does not start and top at distinct vertices.)
1. Did the undirected graph of the 48 states have a Hamiltonian Cycle? Did it have a Hamiltonian Path?
2. If you had a Hamiltonian Cycle in a Graph, explain how you could get a Hamiltonian Path.
3. Does a complete graph always have a Hamiltonian Cycle?
4. Let TS stand for the Traveling Salesman Problem. We proved something involving HC and TS. What was it?
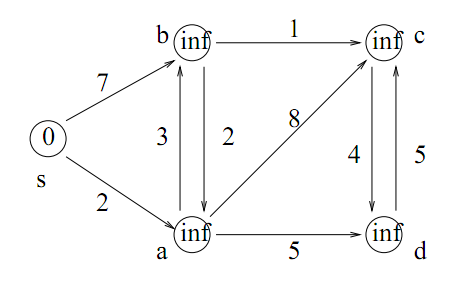
(20) Bin Packing: The Bin Packing Problem (BP) starts with a set of n items, where the size b_i of the ith item is a positive integer. We also start with a number k of bins, all of size a positive integer W. The decision problem asks if we can pack all n objects into k bins. (A "Yes" or "No" answer.) The BP decision problem is NP-complete.
1. Suppose we could solve the BP decision problem in time O(P(n)) for some polynomial p in the variable n. Explain how we could then find the minimum number of bins required in time O(P(n)*log(m)), where m is a number of bins that easily accommodates all the objects.
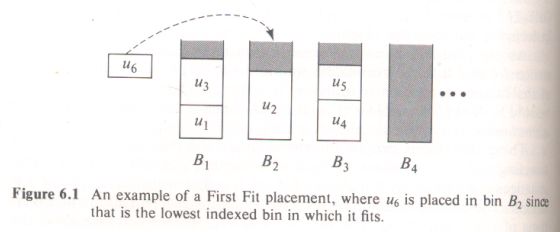
2. There are several algorithms with give an approximate answer to bin packing, though not the exact optimal answer. One of these algorithms is called First Fit (FF). It assumes that we have an arbitrarily long sequence of bins of capacity W. The algorithm places objects into the bins, processing objects in the order b₁,b₂,b₃,... and placing each object into the bin with lowest index into which it will fit. Here's an illustration of this (where in this picture sizes are denoted by u_i):
  
  Denote by OPT(P) the optimal number of bins needed for a BP problem P. Then let FF(P) be the number of bins required by FF. You should show that FF(P) requires at most 2*OPT(P)+1 bins. [Hint: every bin except one must be more than half full. Try to draw a picture in which several bins are half full or less.]