CS3343, Fall 2012, Final Exam, 13 Dec 2012
ANSWERS

  1. (20) Use the Master Theorem to analyze each of the following recurrences. (The theorem may not work for some of them.)

    Recurrences, solution by Master Method, Examples
    Recurrenceab logb(a)nlogb(a) f(n)CaseBehavior
    a. T(n) = 32 T(n / 2) + n2 log(n) 32 2log2(32) = 5 n5n2 log(n) 1 Θ(n5)

    b. T(n) = 2 T(n / 4) + √n log(n) 2 4log4(2) = 1/2 n1/2 = √n √n log(n) noneMaster fails

    c. T(n) = 2 T(n / 2) + n2 2 2log2(2) = 1 n1n2 3 Θ(n2)

    d. T(n) = 16 T(n / 4) + n2 16 4log4(16) = 2 n2n2 2 Θ(n2 log(n))

  2. (10) Strassen's Method for Matrix Multiplication: Consider multiplication of 5-by-5 matrices.
    1. How many scalar multiplications would be required to multiply 5-by-5 matrices using ordinary matrix multiplication? (Justify your answer.) [Each inner product takes 5 mults, and there are 5*5 = 25 such, so there are 5*5*5 = 1254 mults altogether.]

    2. Suppose one could multiply 5-by-5 matrices using 91 scalar multiplications. Give the recurrence for a divide-and-conquer algorithm that would use this fact to multiply matrices of size n-by-n where n is a power of 5. [The recurrence in this case would be T(n) = 91 * T(n/5) + Θ(n2).]

    3. Use the Master Method (or some other approach) so get the asymptotic performance in this case. (You may leave the answer in terms of logarithms.) [The Master Method gives performance of Θ(nlog5(91)). You weren't required to go beyond Θ(nlog5(91)), but this is equal to Θ(n2.8027545). In comparison, Strassen's method gives Θ(nlog2(7)) = Θ(n2.8073549)]

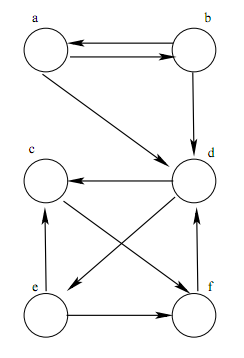
  1. (25) Breadth-First and Depth-First Searches of Graphs: By hand, run through a BFS and a DFS for the graph below, starting with vertex a. Assume that vertices are ordered alphabetically in the adjacency lists. Show the vertices in the order that they are visited. For each search you must use a stack or a queue, whichever is appropriate, but should not use recursion for this problem. For each search and at each step you must show the contents of the stack or the queue.

[For BFS, the order of vertices visited is: a,b,d,c,e,f. For DFS, the order of vertices visited is: a,d,e,f,c,b.]

Queue: add at right, remove from left
BFS QueueActionAdd to Queue
aRemove a and visit aAdd b, d
b dRemove b and visit bAdd -
dRemove d and visit dAdd c, e
c eRemove c and visit cAdd f
e fRemove e and visit eAdd -
fRemove f and visit fAdd -
   
Stack: push at right, remove from right
DFS StactActionPush on Stack
aPop a and visit aPush b, d
b dPop d and visit dPush c, e
b c ePop e and visit ePush f
b c fPop f and visit fPush -
b cPop c and visit cPush -
bPop b and visit bPush -

  1. (25) Dijkstra's Algorithm: Here is a graph to which you should apply Dijkstra's algorithm by hand. This includes deciding on the predecessor of each vertex (= node) as well as the distance from the source vertex (the pi and d fields). In this example the nodes are named (s, a, b, ...) rather than numbered. The source vertex is s. You should fill in each square in the table beside the graph with the currenct integer distance and the current predessor vertex. (You can also give your answer in another way, without the table, but you must be sure to show intermediate steps, especially the relax steps.)

     
    Action Contents of Priority Queue (* = removed)
    Remove
    & Relax    		sabc d
    Initial0, nil∞, nil ∞, nil∞, nil ∞, nil
    rem s* 0, nil2, s7, s ∞, nil∞, nil
    rem a* 0, nil* 2, s5, a 10, a7, a
    rem b* 0, nil* 2, s* 5, a 6, b7, a
    rem c* 0, nil* 2, s* 5, a * 6, b7, a
    rem d* 0, nil* 2, s* 5, a * 6, b* 7, a

  2. (10) Adjacency List: Sketch a picture of the internal adjacency list representation of the graph in problem 4 above. [This is trivial.]

  3. (30) Alternative Topological Sort (using the vertex in-degree) [From your text, page 615] "Another way to perform topological sorting on a directed acyclic graph G = (V, E) is to repeatedly find a vertex of in-degree 0, output it, and remove it and all its outgoing edges from the graph. Explain how to implement this idea so that it runs in time O(V + E). What happens to this algorithm if G has cycles?" Here "in-degree" of a given vertex means the number of edges coming into the vertex. For example, in the graph below, vertex m has in-degree 0 (no edges coming in), while q has in-degree 2 (2 edges coming in; the number of edges going out makes no difference).

    1. First carry out this algorithm by hand on the dag above. [Hint: make a list of the vertices, from m to z. Beside or below each vertex, write its in-degree. Now proceed carefully, step-by-step, keeping track of the current status of each vertex.] [Wow! This was a huge amount of work. Hopefully at the exam I've already told you to just do the first three vertices, and pictorially in the diagram.]

      Vertices  m  n  o   p  q  r   s  t  u   v  w  x   y  z 
      Initial 002 023 222 212 12
      Rm: mDec. q,r,x 02 0 1 2 222 21 1 12
      Rm: nDec. o,q,u 1 0 02 22 1 211 12
      Rm: pDec. o,s,z 0 02 121 211 1 1
      Rm: oDec. r,s,v 0 1 021 111 1 1
      Rm: qDec. t 1 0 11 111 1 1
      Rm: sDec. r 0 11 111 11
      Rm: rDec. u,y 1 0 111 01
      Rm: uDec. t 0 111 01
      Rm: tnone 111 01
      Rm: yDec. v 011 1
      Rm: vDec. w,x 0 0 1
      Rm: wDec. z 0 0
      Rm: xnone 0
      Rm: znone

    2. What will happen if the graph has a cycle, and therefore has no topological sort? (How will the algorithm behave if there is a cycle?) [If there's a cycle, you'll get to the point where vertices remain with positive in-degree, but none with in-degree 0.]

    3. Describe an efficient way to calculate the in-degrees of all vertices at the start of an algorithm. (This can be done in O(V + E) time.) Argue that the whole algorithm will be O(V + E). (This means that there is a fixed constant c so that the time will be less than c * (V + E) for all graphs.[First calculate the in-degree of each vertex by cycling once through all edges. (This could even be done while reading in the edges.) Make up a list of all vertices of in-degree zero. (Any list structure will do.) Repeatedly take vertices with in-degree 0 off the list and decrement the in-degree of each vertex they point to. If when decrementing you get another vertex of in-degree 0, add it to the list. Keep going until the list is empty. At that point if all vertices have in-degree 0, then the order of removal from the list is a topological sort. If any vertices with positive in-degree remain, there is a cycle and no topological sort is possible.]

  4. (20) Reductions Involving Arithmetic Problems: Recall that we looked at 4 problems:

    We also used the relation ≤ to mean "efficient reduction".

    1. Of the two relations, Pm ≤ Ps and Ps ≤ Pm, one of them is trivial, and one depends on the formula:

      Which is which? For the relation that is trivial, why do I call it "trivial"? And for the relation that depends on the formula, explain (briefly) how the formula shows that the relation holds. The second one Ps ≤ Pm is trivial because multiplication includes squaring as a special case. If you can multiply, then certainly you can square. For the other direction Pm ≤ Ps, this asks to reduce multiplication to squaring, that is, if you can square (and can add, subtract, and multiply/divide by powers of 2), can you multiply? The formula make this obvious: how you can substitute 3 squares for one multiply.

    2. Use the formula below and the previous one to argue that: Pm ≤ Pr.

    First it is again almost obvious that Ps ≤ Pr: if you can take reciprocals, then by the formula, with 3 reciprocals (plus 2 subtractions and 1 addition), you can square. Next, since we know from part i that Pm ≤ Ps, then transitifity gives Pm ≤ Pr. (We didn't prove transitifity for this relation, but it's true.)

  5. (20) Turing Machine: Consider the following "mystery" program in the language used for our Turing machines:

    Instructions in the Turing Language
    InstructionRepresentation Op
    Code
    print 0 000 0
    print 1 001 1
    move left 010 2
    move right 011 3
    stop 100 4
    if 0 is scanned
     goto i    		 101 0...0 1
        <-i->    		 5
    if 1 is scanned
     goto j    		 110 1...1 0
        <-j->    		 6
    (end marker) 111 -
    		 
    Mystery Program ??
    InstructionRepresentation
     1. print 0
 2. move right
 3. if 1 is scanned goto 2
 4. print 1
 5. move left
 6. if 1 is scanned goto 5
 7. move left
 8. if 0 is scanned goto 7
 9. print 0
10. move left
11. if 1 is scanned goto 10
12. print 1
13. move right
14. if 1 is scanned goto 13
15. move right
16. if 0 is scanned goto 15
17. if 1 is scanned goto 1
18. stop
    (end marker)

Initial   ...0001100011000...
 tape:               |

    000
011
110 11 0
001
010
110 11111 0
010
101 0000000 1
000
010
110 1111111111 0
001
011
110 1111111111111 0
011
101 000000000000000 1
110 1 0
100
111

    1. Explain carefully what this mystery program does. What is its output and what actions does it go through to produce this output? (All tape squares outside those shown are zero.)[As before I had a lot of trouble writing any program at all that would do something non-trivial. Very hard to write a program that will stop.] 
        Original tape looks like:
L = left segment of 1's, M = middle segment of 0's, R = right segment of 1's
All 0's outside these segments, indefinitely far.

      <--L--><--M--><--R-->
...00011...1100...0011...1100...

OK, here is what the program is doing:
1.     Print 0 at left end of R.
2-3.   Scan right to 1 past right end of R.
4.     Print 1 at 1 past right end of R.
5-6.   Scan left to 1 past left end of R (= right end of M).
7-8.   Scan left to 1 past left end of M (= right end of L).
9.     Print 0 at right end of L.
10-11. Scan left to 1 past left end of L.
12.    Print 1 at 1 past left end of L.
13-14. Scan right to 1 past right end of L (= left end of M).
15-16. Scan right to 1 past right end of M (= left end of R).
17.    Now scanning the 1 at left end of R (same position relative to L, M, and R as at start).
       Will always goto step 1.  Start over.


        Effect of 1 time through loop: R and L stay the same length, and
all of R moves right one square, and
all of L moves left one square, and
M has an extra 2 0's.


        As it runs, L and R pushed apart.  Each loop, M has extra 2 0's.
      Here is simulation run of first 100 steps.

    2. Explain what the program would do if the starting tape configuration were the following:

      
Initial   ...00011100111000...
 tape:               |

      The second initial tape configuration produces simulation run of first 100 steps.

      In general, all three numbers, L, M, and R, can be different, independent of one another.. The only constraints are: L >= 1, M >= 0, R >=0. The boundary example is L = 1, M = 0, R = 0, which produces simulation run of first 100 steps.

  6. (10) Example of Polynomial Time Equivalence. Consider the two problems:

    Consider also the two reductions L1 ≤p L2 and L2 ≤p L1.

    L1 ≤p L2 means to reduce the problem of solving L1 to the problem of solving L2. This means that we start with an instance of L1 and try to find a corresponding instance of L2 is such a way that the solution to the L2 instance gives us the solution to the L1 instance.

    Another way to say this is that assuming we can solve problems in L2, does that let us solve problems in L1?

    1. One of these reductions is trivial. Which one is "trivial" and why do I use that word.?The direction L1 ≤p L2 is the trivial one, because if we can take the square root of any positive number, we can certainly take the square root of any number in the range 1/4 <= x <= 1. Another way to say this is: given any desired sqrt(x) in the range 1/4 <= x <= 1, we associate it with exactly the same problem in the greater range, x > 0. If we can find sqrt(x) for any x > 0, then certainly we can find sqrt(x) for any 1/4 <= x <= 1.

    2. The other is something that we proved. What rough technique did we use to prove it? To prove the other direction: L2 ≤p L1, we start knowing that we can find sqrt(x) in the range 1/4 <= x <= 1. We start with an arbitrary sqrt(x), where x > 0. In this case we normalized the arbitrary case by multiplying or dividing repeately by 4, until our arbitrary problem was in the range 1/4 <= x <= 1. Then take the square root. Finally by dividing or multiplying by 2 to the same power as for normalization, we denormalize and get a solution to original square root.

  7. (10) Hamiltonian Cycles and Paths: Recall that a Hamiltonian Cycle (HC) is a path in an undirected graph that includes all vertices exactly once, and starts and ends at the same vertex. A Hamiltonian Path (HP) is a path that also includes all vertices exactly once, but it starts and ends at distinct vertices. (In this notation, an HC is not an HP, because an HC does not start and top at distinct vertices.)

    1. Did the undirected graph of the 48 states have a Hamiltonian Cycle? Did it have a Hamiltonian Path? It has many Hamiltonian Paths, but no Hamiltonian Cycles.

    2. If you had a Hamiltonian Cycle in a Graph, explain how you could get a Hamiltonian Path. Start with a Hamiltonian Path and delete any edge. Then you have a Hamiltonian Cycle.

    3. Does a complete graph always have a Hamiltonian Cycle? Yes, obviously, since you can proceed from any vertex to any other on an edge (complete=all edges exist). We can traverse the vertices in any order and return to our starting vertex.

    4. Let TS stand for the Traveling Salesman Problem. We proved something involving HC and TS. What was it? We proved that HC ≤p TS.

  8. (20) Bin Packing: The Bin Packing Problem (BP) starts with a set of n items, where the size bi of the ith item is a positive integer. We also start with a number k of bins, all of size a positive integer W. The decision problem asks if we can pack all n objects into k bins. (A "Yes" or "No" answer.) The BP decision problem is NP-complete.

    1. Suppose we could solve the BP decision problem in time O(P(n)) for some polynomial p in the variable n. Explain how we could then find the minimum number of bins required in time O(P(n)*log(m)), where m is a number of bins that easily accommodates all the objects. Start with a specific instance of BP with bound K, call it, say (bp, bound K). Pick a bound M large enough so that (bp, bound M) = "yes". (For example, we could use M = number of objects.) If (bp, bound 0) = "yes" we are done. (This might be a problem with all sizes 0.) Now this proceeds in a way similar to binary search: 
        We have the optimal value trapped between bounds L < R,
where initially L = 0 and R = M.  Set Mid = (L + R)/2.

     L ("no")      Mid (?)       R("yes")
     |--------------|------------|

if the bound of Mid gives a "yes" then change to:

     L ("no")       R ("yes)   
     |--------------|------------|

and if bound of Mid gives a "no" then change to:
                   L ("no")     R ("yes)   
     |--------------|------------|

In this way the optimal value is trapped between bounds
whose distance apart in halved at each stage.  So in
log2(M) steps, we will have the optimal value.

    2. There are several algorithms with give an approximate answer to bin packing, though not the exact optimal answer. One of these algorithms is called First Fit (FF). It assumes that we have an arbitrarily long sequence of bins of capacity W. The algorithm places objects into the bins, processing objects in the order b1,b2,b3,... and placing each object into the bin with lowest index into which it will fit. Here's an illustration of this (where in this picture sizes are denoted by ui):

      Denote by OPT(P) the optimal number of bins needed for a BP problem P. Then let FF(P) be the number of bins required by FF. You should show that FF(P) requires at most 2*OPT(P)+1 bins. [Hint: every bin except one must be more than half full. Try to draw a picture in which several bins are half full or less.] [This is hard stuff!] Any 2 bins that are half full or less can be consolidated into 1 bin. Consider a first fit packing of objects into bins. All but one of these bins must be greater than half full, because otherwise we could consolidate bins. This means that

        FF(P) < 2 * sum(si: all i) + 1

      But all the object must fit into OPT(P) many bins.

        sum( si: all i) <= OPT(P)

      Combining inequalities gives:

        FF(P) < 2 * sum(si: all i) + 1 <= 2 * OPT(P) + 1