CS3343, Spring 2012, Final Exam, 7 Apr 2012       Your Name:                                                                                 
Last First

Directions: Do not spend too much time on any one problem. Try to give as short an answer as you can that still fully answers the question.

  1. (15) Hashing:
    1. Show the result of inserting the following strings into a hash table using the given hash function values shown. They should be inserted in the order given, using open addressing to resolve collisions, and proceeding to the next lower address on each collision: hash(ralph)=8, hash(henry)=10, hash(wayne)=8, hash(roger)=10, hash(hamish)=9, hash(hortense)=7.

    2. What would happen if we deleted the entry for wayne? (That is, made it an empty entry, ready for a new insertion.)

    3. What is wrong with the following hash function, used for a hash table of size 50, where the keys are character strings. (The s.charAt(0) will use the Ascii code for the 0th character, so there's nothing wrong with that.)

      int m = 50; // size of hash table

public int hash(String s, int p, int m) {
   return (s.charAt(0) + s.charAt(s.length()-1))%m;
}

  2. (25) Quicksort and Randomization:
    1. Give the algorithm that randomizes the order of the elements in an array. What is it's asymptotic (time) performance?
    2. What is the worst-case asymptotic (time) performance of quicksort?
    3. Explain how you could use Part i above to improve the performance of quicksort. What kind of time performance does this give? What "awkward" input case(s) does this help with? Does this step eliminate these cases altogether? If not, then why and how does this step help?
    4. Explain how the same technique would eliminate some of the same "awkward" input cases if one used a binary search tree for sorting. Also: how would you use a binary search tree for sorting? What kind of performance does this "tree sort" algorithm have?
    5. Your text's Randomized Quicksort is different from Parts i and iii above. Explain the additions to the quicksort algorithm that give Randomized Quicksort.

  3. (10) Adjacency List: Show the internal adjacency list representation of the graph in problem 4 below.

  4. (25) Breadth-First and Depth-First Searches of Graphs: By hand as we did in Recitation 13, run through a BFS and a DFS for the graph below, starting with vertex a. Assume that vertices are ordered alphabetically in the adjacency lists. Show the vertices in the order that they are visited. For each search you must use a stack or a queue, whichever is appropriate. Show the insertions and removals for each case. In each case the sequence of removals should be your final answer.

  5. (25) Dijkstra's Algorithm: By hand, run through Dijkstra's algorithm on the graph below, starting with vertex a. You should fill in the squares in the table below the graph, giving your answer. (You can also give your answer in another way, without the table, but you must be sure to show intermediate steps, especially the relax steps.)

     
    Action Contents of Priority Queue (* = removed)
    Remove
    & Relax    		abc d ef
    Initial0∞∞∞ ∞∞
            
            
            
            
            
            

  6. (20) Problems in NP:
    1. Is any problem in P (polynomial-time problems) also in NP?
    2. Is P the same as NP? Can you prove this?
    3. Give the "guessing-stage / checking-stage" definition that shows a problem is in NP.
    4. How would you use the definition in (iii) above to show that the problem Subset Sum (SS) is in NP? Here you start with a set A of positive integers and a given sum S. The problem is whether or not A has a subset A' whose numbers add up to S.

     

     

  7. (20) Turing Machine: Consider the following "mystery" program in the language used for our Turing machines:

    Instructions in the Turing Language
    InstructionRepresentation Op
    Code
    print 0 000 0
    print 1 001 1
    move left 010 2
    move right 011 3
    stop 100 4
    if 0 is scanned
     goto i    		 101 0...0 1
        <-i->    		 5
    if 1 is scanned
     goto j    		 110 1...1 0
        <-j->    		 6
    (end marker) 111 -
    		 
    Mystery Program ??
    InstructionRepresentation
     1. print 0
 2. move right
 3. if 1 is scanned goto 2
 4. print 1
 5. move left
 6. if 1 is scanned goto 5
 7. move left
 8. if 0 is scanned goto 7
 9. print 0
10. move left
11. if 1 is scanned goto 10
12. print 1
13. move right
14. if 1 is scanned goto 13
15. move right
16. if 0 is scanned goto 15
17. if 1 is scanned goto 1
18. stop
    (end marker)

Initial   ...0001100011000...
 tape:               |

    000
011
110 11 0
001
010
110 11111 0
010
101 0000000 1
000
010
110 1111111111 0
001
011
110 1111111111111 0
011
101 000000000000000 1
110 1 0
100
111

    1. Explain carefully what this mystery program does. What is its output and what actions does it go through to produce this output? (All tape squares outside those shown are zero.)

    2. Suppose the starting tape configuration were the following:

      
Initial   ...00011100111000...
 tape:               |

  8. (20) Example of Polynomial Time Equivalence. Consider the two problems:

    Consider also the two reductions L1 ≤p L2 and L2 ≤p L1.

    1. One of these reductions is trivial. Which one is "trivial" and why do I use that word.?
    2. The other is something that we proved. What rough technique did we use to prove it?

  9. (20) Hamiltonian Cycles and Paths: Recall that a Hamiltonian Cycle (HC) is a path in an undirected graph that includes all vertices exactly once, and starts and ends at the same vertex. A Hamiltonian Path (HP) is a path that also includes all vertices exactly once, but it starts and ends at distinct vertices. (In this notation, an HC is not an HP, because an HC does not start and top at distinct vertices.)

    1. Did the undirected graph of the 48 states have a Hamiltonian Cycle? Did it have a Hamiltonian Path?

    2. If you had a Hamiltonian Cycle in a Graph, explain how you could get a Hamiltonian Path.

    3. Does a complete graph always have a Hamiltonian Cycle?

    4. Let TS stand for the Traveling Salesman Problem. We proved something involving HC and TS. What was it?

  10. (20) Bin Packing: The Bin Packing Problem (BP) starts with a set of n objects, where the size si of the ith object satisfies 0 < si < 1. We also start with a number K of unit-size bins. The decision problem asks (with a "Yes" or "No" answer) if we can pack all n objects into K bins. The BP decision problem is NP-complete. (We visualize that objects and bins all have base a unit square, and so all that matters is the height. For example, we can fit 8 objects of size 0.25 into 2 bins, by piling 4 into each bin.)

    1. State an optimization problem that corresponds to the decision problem above.

    2. If we could solve the BP decision problem in time O(P(n)) for some polynomial p in the variable n, explain how we could solve the optimization problem in time O(P(n)*log(M)), where M is a number of bins that easily accommodates all the objects.

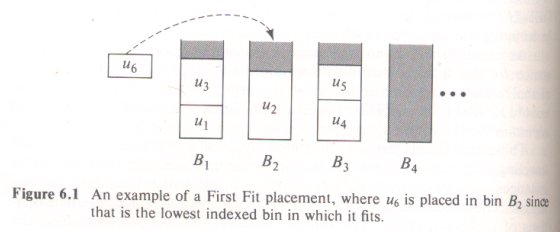
    3. There are several algorithms with give an approximate answer to bin packing, though not the exact optimal answer. One of these algorithms is called First Fit (FF). It assumes that we have an infinite sequence B1,B2,B3,... of unit-capacity bins. The algorithm places objects int the bins, processing objects in the order s1,s2,s3,... and placing each object into the bin with lowest index into which it will fit. Here's an illustration of this (where in this picture sizes are denoted by ui):

      Denote by OPT(P) the optimal number of bins needed for a BP problem P. Then let FF(P) be the number of bins required by FF. You should show that FF(P) requires at most 2*OPT(P)+1 bins. [Hint: every bin except one must be more than half full. Try to draw a picture in which several bins are half full or less.]

      There is an approximation algorithm First Fit Decreasing that handles the objects in decreasing order of size. Anyone who had packed up a truck for moving knows that this is likely to give better results, and it does.