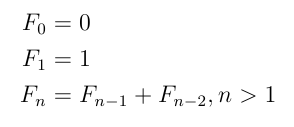
CS3343/3341 Analysis of Algorithms Spring 2012 Weird Topic |
Binary, Ternary, and Fibonacci Searches |
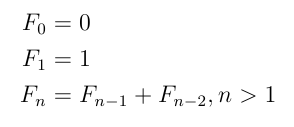
| Binary, Ternary, Fibonacci Search | ||
|---|---|---|
public int binarySearch(double[] A, double y) {
int low = 1;
int high = A.length - 1;
while (low <= high) {
int mid = (low + high)/2;
if (A[mid] == y) return mid; // found
else if (A[mid] < y) low = mid + 1;
else high = mid - 1;
}
return -1; // not found
}
|
public int ternarySearch(double[] A, double y) {
int low = 1;
int high = A.length - 1;
while (low <= high) {
int mid = (2*low + high)/3;
if (A[mid] == y) return mid; //found
else if (A[mid] > y) high = mid - 1;
else {
low = mid + 1;
mid = (low + high)/2;
if (A[mid] == y) return mid;// found
else if (A[mid] > y) high = mid -1;
else low = mid + 1;
}
}
return -1; // not found
}
|
// Fibonacci search, search A[1],...,A[N]
// Here N+1 must be a Fib. number, F[m+1]
int N = F[m+1] - 1; // Fibonacci number - 1
int Np = F[m]; // previous Fibonacci number
public int fibonacciSearch(double[] A, double y) {
int mid = Np; // F[m]
int p = (N+1) - Np; // F[m-1]
int q = 2*Np - (N+1); // F[m-2]
for (;;) {
if (y == A[mid]) return mid; // found
else if (y < A[mid]) {
if (q == 0) return -(mid - 1);// not
mid = mid - q;
int temp = p;
p = q;
q = temp - q;
}
else if (y > A[mid]) {
if (p == 1) return -mid;// not found
mid = mid + q;
p = p - q;
q = q - p;
}
}
}
|