 |
Advanced Programming
Spring 2005
Recitation 14: Graph Algorithms
Week 14: Apr 26-28
Due (on time): 2005-05-03 23:59:59
Due (late): 2005-05-08 23:59:59
|
CS 2213/2211 Advanced Programming Spring 2005 Recitation 14: Graph Algorithms Week 14: Apr 26-28 Due (on time): 2005-05-03 23:59:59 Due (late): 2005-05-08 23:59:59 |
Recitation 14 should be submitted
following directions at: submissions with deadlines
|
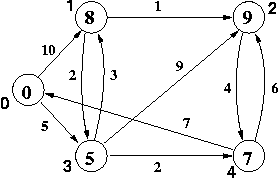 |
The algorithm will be illustrated by the example graph at the left. There are 5 vertices, represented as circles and numbered 0, 1, 2, 3, 4, and 5, with a number just outside the circle. Directed edges are given as an arrow from one edge to another, and the weights are given as a number near the center of the arrow.
The numbers inside the circles are the distances of the shortest path from vertex 0 to the given vertex. These numbers are what your program is supposed to calculate for this recitation. Of course vertex 0 has distance 0 from itself. You can get to vertex 2 in three steps by going from 0 to 3 (weight 5), then from 3 to 1 (weight 3), and then from 1 to 2 (weight 1). So the sum of the three weights on the corresponding edges are 5 + 3 + 1 = 9, so this 9 appears inside the circle representing vertex 2, since this is the shortest path (although that might not be immediately obvious).
0 1 10 0 3 5 1 2 1 1 3 2 2 4 4 3 1 3 3 2 9 3 4 2 4 0 7 4 2 6
#define N 5 /* for this particular graph */
struct gnode { /* node in the linked list following each vertex */
int v; /* vertex at the other end (at the arrow) */
int dist; /* the weigth on this edge */
struct gnode *next; /* next vertex in the linked list */
};
struct gnode *g[N]; /* the graph: an array of pointers to the list nodes */
int status[N]; /* vertex has not been processed (0) or has been (1) */
int shortest[N]; /* final length of the shortest path to each vertex */
|
You are permitted to deviate from the above if you want, as long as you're not copying from some existing program. For example, I am suggessting three "parallel" arrays above for simplicity, but a better way might be to use a single array of structs with three fields. Assuming you used the above notation, here is code that will "dump" the adjacency list that you should create, along with the output. (You do not need to use this code.)
void dumpgraph(struct gnode *g[]) {
int i;
struct gnode *p;
for (i = 0; i < N; i++) {
printf("g[%i]: ", i);
p = g[i];
while (p != NULL) {
printf("--> (%i,%i) ",
p -> v, p -> dist);
p = p -> next;
}
printf("--> NULL\n");
}
} | g[0]: --> (3,5) --> (1,10) --> NULL g[1]: --> (3,2) --> (2,1) --> NULL g[2]: --> (4,4) --> NULL g[3]: --> (4,2) --> (2,9) --> (1,3) --> NULL g[4]: --> (2,6) --> (0,7) --> NULL |
The array int status[N]; should be initialized to all 0's. Each of the vertices will be processed, and as the ith vertex is processed, status[i] should be set to 1. The array int shortest[N]; should have each element initialized to the number given by #define MAXPOS 0x7fffffff (this is the largest positive 32-bit number, 231 - 1, effectively infinity), except for vertex 0 which should have its entry, shortest[0] set to 0, since this is the start of paths.
Next, in a loop, you must repeatedly find the next vertex u such that status[u] is still 0 and such that shortest[u] <= shortest[v] for any other vertex v with status[v] == 0. Once you find such a u, first change status[u] to 1. Then look at any vertex w, where status[w] is 0 and (u, w) is a directed edge. Let d be the weight of this edge. If shortest[u] + d is less than shortest[w], then let this be the new value of shortest[w]. Keep going this way, "using up" a vertex each loop, until no more remain. Then the shortest array gives the lengths of the shortest paths.
The whole algorithm above is illustrated and described on the following page: Example graph.
|
Contents of email submission
for Recitation 14: Last Name, First Name; Course Number; Recitation Number. a. Source code for your program for this recitation. b. Results of invoking the dumpgraph function (or a similar function that matches your own code), to show that your adjacency list representation is correct. c. Rest of the run giving the final shortest path lengths. Debug output similar to what I gave above would be welcome. d. Run the program again with the same graph, but this time using vertex 2 (TWO) as the distinguished vertex. That is, find the lengths of the shortest paths from vertex 2 to every vertex. (In your program, you will need to set shortest[2] equal to 0, and the remaining values equal to MAXPOS == 0x7fffffff. It's easy to check by hand whether your answer is correct.) e. (Just for fun) Here is data about a larger undirected graph: cities2.dat. Read the edges and insert a directed edge in each direction with the given weight. (Two edges inserted for each line read.) These are the 22 state capitols west of the Mississippi: citynames2.dat. (I put Topeka, Kansas out of alphabetic order because it's my home town (which might explain a number of things about me).) Run the program and find out how far each of the capitols is from Topeka. (Here is a picture of this data, which is being used to explain a different problem: PDF, JPG.)
|